อินดักเตอร์อนุกรมและขนาน (สูตรและตัวอย่างปัญหา)

ฟิลด์: ไฟฟ้าพื้นฐาน

China

อินดักเตอร์คืออะไร?

อินดักเตอร์ (หรือเรียกว่าอินดักเตอร์ไฟฟ้า) ถูกกำหนดให้เป็นองค์ประกอบไฟฟ้าแบบพาสซีฟที่มีสองขั้ว ซึ่งเก็บพลังงานในรูปของสนามแม่เหล็กเมื่อกระแสไฟฟ้าไหลผ่าน มันยังถูกเรียกว่าคอยล์ ช็อก หรือเรกเตอร์.

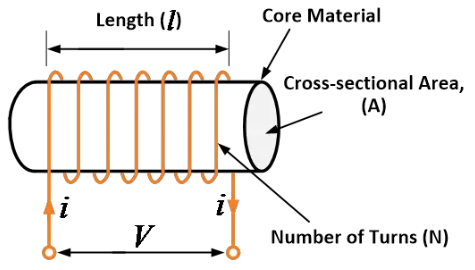
อินดักเตอร์เป็นเพียงแค่วงจรลวดที่พันเป็นวงกลม มันมักจะประกอบด้วยวงจรลวดของวัสดุนำไฟฟ้าโดยปกติจะเป็นทองแดงที่หุ้มฉนวน พันรอบแกนเหล็กที่ทำจากพลาสติกหรือวัสดุเฟอร์โรแมกเนติก; ดังนั้นมันจึงถูกเรียกว่าอินดักเตอร์แกนเหล็ก.

อินดักเตอร์มักจะมีอยู่ในช่วงตั้งแต่ 1 µH (10-6 H) ถึง 20 H หลายอินดักเตอร์มีแกนแม่เหล็กที่ทำจากเฟอร์ไรต์หรือเหล็กภายในวงจรลวด ซึ่งใช้เพื่อเพิ่มสนามแม่เหล็กและดังนั้นความเหนี่ยวนำของอินดักเตอร์.

ตามกฎของฟาราเดย์ของอินดักชันแม่เหล็กไฟฟ้า เมื่อมีการเปลี่ยนแปลงของกระแสไฟฟ้าที่ไหลผ่านอินดักเตอร์หรือคอยล์ สนามแม่เหล็กที่เปลี่ยนแปลงตามเวลาจะสร้างแรงดันไฟฟ้า (e.m.f.) หรือแรงดันในมัน แรงดันหรือ e.m.f. ที่เกิดขึ้นในอินดักเตอร์จะมีความสัมพันธ์ตรงกับอัตราการเปลี่ยนแปลงของกระแสไฟฟ้าที่ไหลผ่านอินดักเตอร์.

อินดักทันซ์ (L) เป็นคุณสมบัติของอินดักเตอร์ที่ขัดขวางการเปลี่ยนแปลงขนาดหรือทิศทางของกระแสไฟฟ้าที่ไหลผ่านมัน อินดักเตอร์ที่มีอินดักทันซ์มากขึ้น จะมีความสามารถในการเก็บพลังงานไฟฟ้าในรูปแบบของสนามแม่เหล็กมากขึ้น

อินดักเตอร์ทำงานอย่างไร?

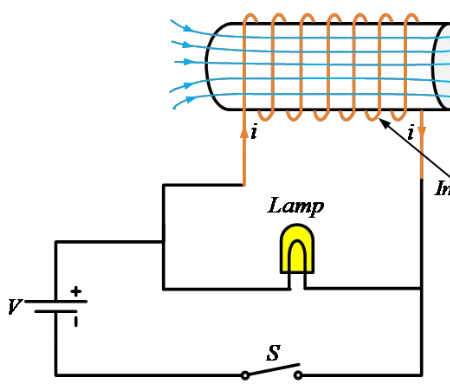
อินดักเตอร์ในวงจรจะขัดขวางการเปลี่ยนแปลงของกระแสไฟฟ้าที่ไหลผ่านโดยทำให้เกิดแรงดันไฟฟ้าขึ้นที่อินดักเตอร์ซึ่งสัดส่วนกับอัตราการเปลี่ยนแปลงของกระแสไฟฟ้า เพื่อทำความเข้าใจว่าอินดักเตอร์ทำงานอย่างไรในวงจร ลองพิจารณาภาพด้านล่าง

ตามที่แสดง หลอดไฟ ขดลวด (อินดักเตอร์) และสวิตช์ถูกเชื่อมต่อกับแบตเตอรี่ หากเราเอาอินดักเตอร์ออกจากวงจร หลอดไฟจะสว่างขึ้นตามปกติ แต่เมื่อมีอินดักเตอร์วงจรจะมีพฤติกรรมที่แตกต่างไป

อินดักเตอร์หรือขดลวดมีความต้านทานต่ำกว่าหลอดไฟมาก ดังนั้นเมื่อปิดสวิตช์กระแสไฟฟ้าส่วนใหญ่จะไหลผ่านขดลวดเนื่องจากเป็นเส้นทางที่มีความต้านทานต่ำ ดังนั้นเราคาดหวังว่าหลอดไฟจะสว่างน้อยลง

แต่เนื่องจากพฤติกรรมของอินดักเตอร์ในวงจร เมื่อปิดสวิตช์ หลอดไฟจะสว่างขึ้นและค่อยๆ ดับลง และเมื่อเปิดสวิตช์ หลอดไฟจะสว่างมากและค่อยๆ ดับลงอย่างรวดเร็ว

สาเหตุคือ เมื่อมีแรงดันหรือความต่างศักย์ที่อินดักเตอร์ กระแสไฟฟ้าที่ไหลผ่านอินดักเตอร์จะสร้างสนามแม่เหล็ก สนามแม่เหล็กนี้จะสร้างกระแสไฟฟ้าเหนี่ยวนำในอินดักเตอร์แต่มีขั้วตรงข้าม ตามกฎของเลนซ์

กระแสไฟฟ้าเหนี่ยวนำที่เกิดจากสนามแม่เหล็กของอินดักเตอร์พยายามขัดขวางการเปลี่ยนแปลงใด ๆ ไม่ว่าจะเพิ่มขึ้นหรือลดลง ของกระแสไฟฟ้า เมื่อสนามแม่เหล็กสร้างเสร็จ กระแสไฟฟ้าสามารถไหลได้ตามปกติ

ตอนที่ปิดสวิตช์ สนามแม่เหล็กรอบอินดักเตอร์จะทำให้กระแสไฟฟ้าไหลผ่านอินดักเตอร์จนกว่าสนามแม่เหล็กจะล้มเหลว กระแสไฟฟ้านี้จะทำให้หลอดไฟสว่างอยู่นานหนึ่งขณะแม้ว่าสวิตช์จะเปิดอยู่

กล่าวอีกนัยหนึ่ง อินดักเตอร์สามารถเก็บพลังงานในรูปแบบของสนามแม่เหล็กและพยายามขัดขวางการเปลี่ยนแปลงของกระแสไฟฟ้าที่ไหลผ่านมัน ดังนั้นผลรวมคือ กระแสไฟฟ้าผ่านอินดักเตอร์ไม่สามารถเปลี่ยนแปลงทันทีได้

สัญลักษณ์วงจรของอินดักเตอร์

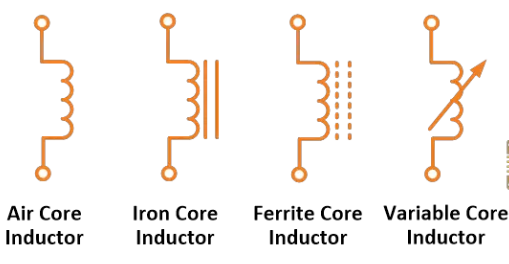
สัญลักษณ์วงจรของอินดักเตอร์แสดงในภาพด้านล่าง

สมการของอินดักเตอร์

แรงดันที่เกิดขึ้นที่อินดักเตอร์

แรงดันที่เกิดขึ้นที่อินดักเตอร์มีความสัมพันธ์โดยตรงกับอัตราการเปลี่ยนแปลงของกระแสไฟฟ้าที่ไหลผ่านอินดักเตอร์ ทางคณิตศาสตร์ แรงดันที่เกิดขึ้นที่อินดักเตอร์สามารถแสดงได้ว่า

$\begin{align*} v_L = L \frac{di_L}{dt} \end{align*}$

โดยที่ $v_L$ = แรงดันทันทีที่เกิดขึ้นที่อินดักเตอร์ในหน่วยโวลต์

$L$ = อิน덕แตนซ์ในหน่วยเฮนรี

$\frac{di_L}{dt}$ = อัตราการเปลี่ยนแปลงของกระแสไฟฟ้าในหน่วยแอมแปร์ต่อวินาที

แรงดันที่เกิดขึ้นที่อินดักเตอร์มาจากพลังงานที่ถูกสะสมในสนามแม่เหล็กของอินดักเตอร์

หากกระแสตรงไหลผ่านอินดักเตอร์ $\frac{di_L}{dt}$ จะเป็นศูนย์ เนื่องจากกระแสตรงมีค่าคงที่ตามเวลา ดังนั้น แรงดันที่เกิดขึ้นที่อินดักเตอร์จะเป็นศูนย์ ดังนั้น ในกรณีที่พิจารณาปริมาณกระแสตรง ในภาวะคงที่ อินดักเตอร์จะทำงานเหมือนวงจรลัดวงจร

กระแสผ่านอินดักเตอร์

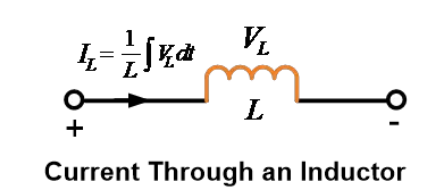
เราสามารถแสดงกระแสผ่านอินดักเตอร์ในรูปของแรงดันที่เกิดขึ้นที่อินดักเตอร์ได้ว่า

$\begin{align*} i_L = \frac{1}{L} \int v_L dt \end{align*}$

ในสมการด้านบน ขอบเขตของการอินทิเกรตถูกกำหนดโดยการพิจารณาประวัติหรือเงื่อนไขเริ่มต้น คือ จาก $-\infty \,\, to \,\, t(0^-)$ .

ตอนนี้ สมมติว่าการเปลี่ยนสถานะเกิดขึ้นที่ t=0 หมายความว่าสวิตช์ถูกปิดที่ t=0 เราจะได้สมการของกระแสผ่านอินดักเตอร์ว่า

$\begin{align*} i_L = \frac{1}{L} \int v_L dt \end{align*}$

เราสามารถแบ่งช่วงการอินทิเกรตออกเป็นสองช่วงได้คือ $-\infty \,\, to \,\, 0$ และ $0 \,\, to \,\,t$ เราทราบว่า $0^-$ เป็นจุดก่อนการเปลี่ยนแปลงเกิดขึ้น ในขณะที่ $0^+$ เป็นจุดหลังจากที่การเปลี่ยนแปลงเกิดขึ้น ดังนั้น เราสามารถเขียนได้ว่า

$\begin{align*} i_L = \frac{1}{L} \int_{-\infty}^{t} v_L dt \end{align*}$

ดังนั้น

$\begin{align*} i_L = \frac{1}{L} \int_{-\infty}^{0^-} v_L dt + \frac{1}{L} \int_{0^-}^{t} v_L dt \end{align*}$

ที่นี่ $\frac{1}{L} \int_{-\infty}^{0^-} v_L dt$ แสดงค่าของกระแสในตัวเหนี่ยวนำในช่วงเวลาที่ผ่านมาซึ่งเป็นสภาพเริ่มต้นของ $i_L$ ให้แทนด้วย $i_L(0^-)$ .

$\begin{align*} i_L = i_L(0^-) + \frac{1}{L} \int_{0^-}^{t} v_L dt \end{align*}$

ที่ $t=0^+$ เราสามารถเขียนได้ว่า

$\begin{align*} i_L (0^+)= i_L(0^-) + \frac{1}{L} \int_{0^-}^{0^+} v_L dt \end{align*}$

เริ่มต้นเราได้สมมติว่าการสลับสวิตช์เกิดขึ้นที่เวลาศูนย์ ดังนั้น การอินทิเกรตจาก $0^-$ ถึง $0^+$ เป็นศูนย์

ดังนั้น

$\begin{align*} i_L(0^-) = i_L(0^+) \end{align*}$

ดังนั้น กระแสผ่านอินดักเตอร์ไม่สามารถเปลี่ยนแปลงได้ทันที นั่นหมายความว่ากระแสผ่านอินดักเตอร์ก่อนและหลังจากการสลับสวิตช์เป็นอย่างเดียวกัน

อินดักเตอร์ที่ t=0

ตัวเหนี่ยวนำที่ $t = 0$ กล่าวคือ ขณะเวลาที่มีการเปิด-ปิดสวิตช์ แรงดันข้ามขดลวดเหนี่ยวนำจะมีค่าเป็น $\infty$ เนื่องจากช่วงเวลา $dt$ เป็นศูนย์ ดังนั้น ขณะเวลาที่มีการเปิด-ปิดสวิตช์ ตัวเหนี่ยวนำจะทำหน้าที่เหมือนวงจรเปิด ในขณะที่ในสภาวะคงที่ที่ $t = \infty$ จะทำหน้าที่เหมือนวงจรลัด

หากตัวเหนี่ยวนำมีกระแสเริ่มต้น I0 ก่อนที่จะมีการเปลี่ยนสถานะ การเปิด-ปิดสวิตช์ แล้วที่ช่วงเวลา $t=0^+$ จะทำหน้าที่เหมือนแหล่งจ่ายกระแสคงที่ที่มีค่าเท่ากับ $I_0$ ในขณะที่ในสภาวะคงที่ที่ $t=\infty$ จะทำหน้าที่เหมือนวงจรลัดข้ามแหล่งจ่ายกระแส

ตัวเหนี่ยวนำแบบอนุกรมและขนาน

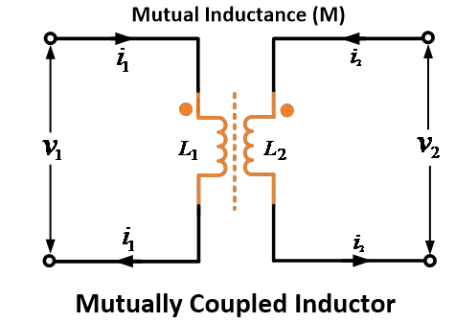
อินดักเตอร์ที่ต่ออนุกรมและขนานมีพฤติกรรมคล้ายกับตัวต้านทานที่ต่ออนุกรมและขนาน ให้พิจารณาสองขดลวดแม่เหล็กที่เชื่อมโยงกัน 1 และ 2 ซึ่งมีความเหนี่ยวนำเอง $L_1$ และ $L_2$ ตามลำดับ ให้ M เป็นความเหนี่ยวนำร่วมระหว่างสองขดลวดในหน่วยเฮนรี

อินดักเตอร์สองตัวในวงจรไฟฟ้าสามารถเชื่อมต่อได้หลายวิธี ซึ่งจะให้ค่าความเหนี่ยวนำเทียบเท่าที่แตกต่างกันตามที่อภิปรายไว้ด้านล่าง

สูตรของอินดักเตอร์ที่ต่ออนุกรม

วิธีการเพิ่มอินดักเตอร์ที่ต่ออนุกรม

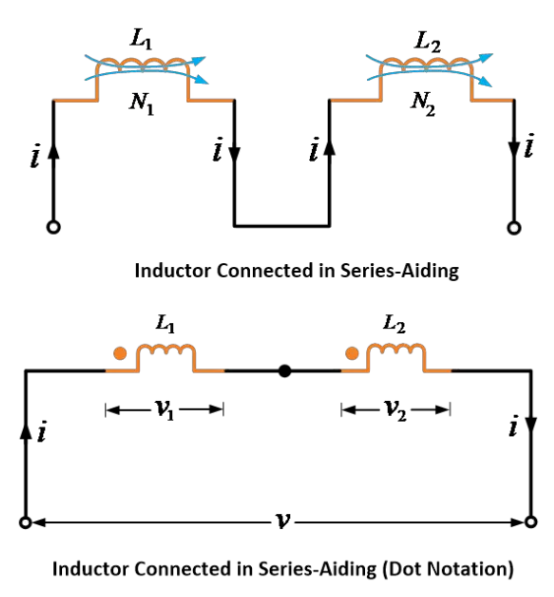
พิจารณาวงจรที่มีอินดักเตอร์หรือขดลวดที่เชื่อมโยงกันสองตัวที่ต่อเป็นอนุกรม มีวิธีการเชื่อมต่ออินดักเตอร์เป็นอนุกรมสองวิธี

ในวิธีแรก ฟลักซ์ที่สร้างโดยอินดักเตอร์ทำงานในทิศทางเดียวกัน ในกรณีนี้ อินดักเตอร์ถูกเรียกว่าต่อแบบช่วยเสริมหรือต่อแบบสะสม
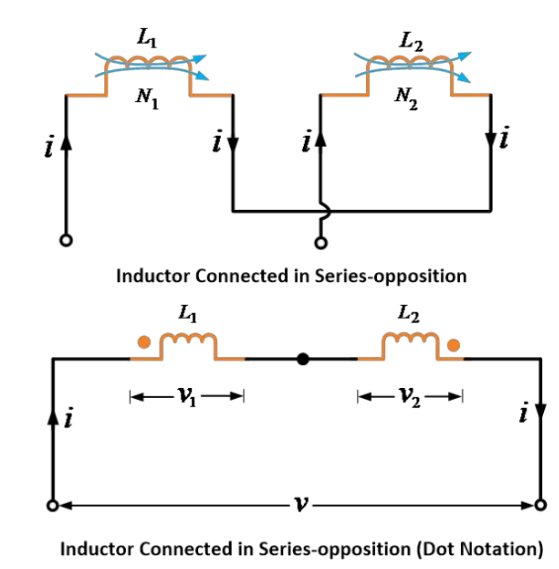
ในวิธีที่สอง หากกระแสในอินดักเตอร์อีกตัวหนึ่งถูกกลับทิศทางทำให้ฟลักซ์ที่สร้างโดยอินดักเตอร์ต้านกัน ในกรณีนี้ อินดักเตอร์ถูกเรียกว่าต่อแบบต้านหรือต่อแบบแยก

ให้ความเหนี่ยวนำของตัวเหนี่ยวนำที่ 1 เป็น $L_1$ และความเหนี่ยวนำของตัวเหนี่ยวนำที่ 2 เป็น $L_2$ ทั้งสองตัวเหนี่ยวนำถูกเชื่อมโยงด้วย ความเหนี่ยวนำร่วม M.

การเชื่อมต่อแบบช่วยเสริม (Cumulative) (แรงดันไฟฟ้าที่เกิดจากความเหนี่ยวนำร่วมช่วยเสริมแรงดันไฟฟ้าที่เกิดจากความเหนี่ยวนำตนเอง)

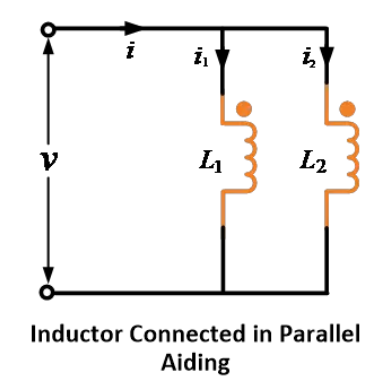
ตัวเหนี่ยวนำหรือขดลวดทั้งสองถูกเชื่อมต่อแบบช่วยเสริมหรือแบบสะสม ตามภาพด้านล่าง

ในการเชื่อมต่อนี้ ฟลักซ์แม่เหล็กที่เกิดจากความเหนี่ยวนำตนเองและฟลักซ์แม่เหล็กที่เกิดจากความเหนี่ยวนำร่วมของตัวเหนี่ยวนำทั้งสองทำงานในทิศทางเดียวกัน ดังนั้น แรงดันไฟฟ้าที่เกิดจากความเหนี่ยวนำตนเองและแรงดันไฟฟ้าที่เกิดจากความเหนี่ยวนำร่วมจึงอยู่ในทิศทางเดียวกัน

ดังนั้น

แรงดันไฟฟ้าที่เกิดจากความเหนี่ยวนำตนเองในตัวเหนี่ยวนำที่ 1, $e_s_1 = -L_1\frac{di}{dt}$
แรงดันไฟฟ้าที่เกิดจากความเหนี่ยวนำร่วมในตัวเหนี่ยวนำที่ 1, $e_m_1 = -M\frac{di}{dt}$
แรงดันไฟฟ้าที่เกิดจากความเหนี่ยวนำตนเองในตัวเหนี่ยวนำที่ 2, $e_s_2 = -L_2\frac{di}{dt}$
แรงดันไฟฟ้าที่เกิดจากการเหนี่ยวนำร่วมในอินดักเตอร์ 1, $e_m_2 = -M\frac{di}{dt}$

แรงดันไฟฟ้าที่เกิดจากการเหนี่ยวนำรวม,

$\begin{align*} e=-(L_1\frac{di}{dt}+M\frac{di}{dt}+L_2\frac{di}{dt}+M\frac{di}{dt}) \end{align*}$

(1) $\begin{equation*} e = -(L_1+L_2+2M) \frac{di}{dt} \end{equation*}$

ถ้า $L_eq$ คือความต้านทานเหนี่ยวนำที่เท่ากันของสองอินดักเตอร์ในวงจรเชื่อมต่อแบบช่วยเสริม แรงดันไฟฟ้าที่เกิดจากการเหนี่ยวนำในวงจรรวมจะเป็นไปตาม,

(2) $\begin{equation*} e = -L_e_q_. \frac{di}{dt} \end{equation*}$

เมื่อเปรียบเทียบสมการ (1) และ (2) เราได้,

(3) $\begin{equation*} L_e_q_. = L_1 + L_2 + 2M \end{equation*}$

สมการด้านบนให้ค่าความเหนี่ยวนำที่เทียบเท่าของสองอินดักเตอร์หรือขดลวดที่เชื่อมต่อกันแบบสะสมหรือเพิ่มเข้าด้วยกัน

หากไม่มีความเหนี่ยวนำร่วมระหว่างสองขดลวด (กล่าวคือ M = 0) แล้ว

$\begin{align*} L_e_q_. = L_1 + L_2 \end{align*}$

การเชื่อมต่อแบบอนุพันธ์ (Differential) (แรงดันไฟฟ้าที่เกิดจากการเหนี่ยวนำร่วมต้านแรงดันไฟฟ้าที่เกิดจากการเหนี่ยวนำตนเอง)

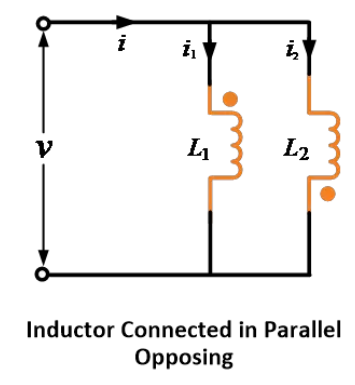
พิจารณาวงจรที่มีอินดักเตอร์หรือขดลวดที่เชื่อมต่อกันในชุดที่ทำให้ฟลักซ์ที่สร้างโดยสองอินดักเตอร์ต้านกัน ดังแสดงในภาพด้านล่าง

เนื่องจากฟลักซ์ต้านกัน ดังนั้นเครื่องหมายของแรงดันไฟฟ้าที่เกิดจากการเหนี่ยวนำร่วมจะตรงข้ามกับแรงดันไฟฟ้าที่เกิดจากการเหนี่ยวนำตนเอง ดังนั้น

แรงดันไฟฟ้าที่เกิดจากการเหนี่ยวนำตนเองในอินดักเตอร์ 1, $e_s_1 = -L_1\frac{di}{dt}$
แรงดันไฟฟ้าที่เหนี่ยวนำซึ่งกันและกันในอินดักเตอร์ 1, $e_m_1 = +M\frac{di}{dt}$
แรงดันไฟฟ้าที่เหนี่ยวนำเองในอินดักเตอร์ 2, $e_s_2 = -L_2\frac{di}{dt}$
แรงดันไฟฟ้าที่เหนี่ยวนำซึ่งกันและกันในอินดักเตอร์ 2, $e_m_2 = +M\frac{di}{dt}$

แรงดันไฟฟ้าที่เหนี่ยวนำรวมในวงจร,

$\begin{align*} e=-(L_1\frac{di}{dt}-M\frac{di}{dt}+L_2\frac{di}{dt}-M\frac{di}{dt}) \end{align*}$

(4) $\begin{equation*} e = -(L_1+L_2-2M) \frac{di}{dt} \end{equation*}$

ถ้า $L_e_q$ เป็นความต้านทานเหนี่ยวนำที่เทียบเท่าของอินดักเตอร์สองตัวที่เชื่อมต่อแบบอนุกรมตรงข้าม แรงดันไฟฟ้าที่เหนี่ยวนำในวงจรคือ,

(5) $\begin{equation*} e = -L_e_q_. \frac{di}{dt} \end{equation*}$

เปรียบเทียบสมการ (4) และ (5) เราจะได้

(6) $\begin{equation*} L_e_q_. = L_1 + L_2 - 2 M \end{equation*}$

สมการข้างต้นแสดงค่าความเหนี่ยวนำเทียบเท่าของขดลวดสองขดที่ต่อแบบอนุกรมตรงข้ามหรือการต่อแบบต่างศักย์

หากไม่มีความเหนี่ยวนำร่วมกันระหว่างขดลวดทั้งสอง (กล่าวคือ M = 0) จะได้

$\begin{align*} L_e_q_. = L_1 + L_2 \end{align*}$

ตัวอย่างที่ 1

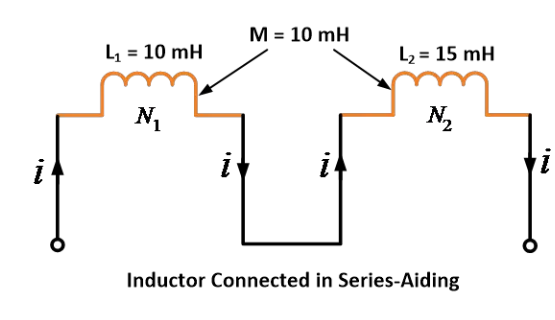
ขดลวดสองขดมีความเหนี่ยวนำตัวเอง 10 mH และ 15 mH ตามลำดับ และมีความเหนี่ยวนำร่วมกัน 10 mH จงหาค่าความเหนี่ยวนำเทียบเท่าเมื่อเชื่อมต่อแบบอนุกรมช่วยกัน

วิธีการแก้:

ข้อมูลที่ให้มา: L1 = 10 มิลลิเฮนรี, L2 = 15 มิลลิเฮนรี และ M = 10 มิลลิเฮนรี

ตามสูตรการเชื่อมต่อแบบช่วยเสริมซีรีส์

$\begin{align*} \begin{split} & L_e_q_. = L_1 + L_2 + 2M \\ & = 10 + 15 + 2(10) \\ & = 10 + 15 + 20 \\ & L_e_q_. = 45\,\,mH \end{split} \end{align*}$

ดังนั้น โดยใช้สมการ เราจะได้อิน덕턴ซ์เทียบเท่า 45 มิลลิเฮนรีเมื่อเชื่อมต่อในรูปแบบช่วยเสริมซีรีส์

ตัวอย่างที่ 2

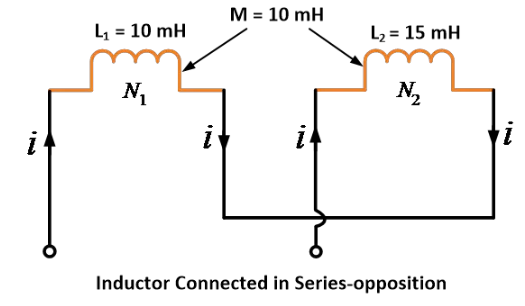
วงจรสองวงมีอิน덕턴ซ์เองคือ 10 มิลลิเฮนรีและ 15 มิลลิเฮนรี และอิน덕턴ซ์ระหว่างวงจรสองวงคือ 10 มิลลิเฮนรี หาอิน덕턴ซ์เทียบเท่าเมื่อเชื่อมต่อในรูปแบบตรงกันข้าม

วิธีการแก้:

ข้อมูลที่ให้มา: L1 = 10 มิลลิเฮนรี, L2 = 15 มิลลิเฮนรี และ M = 10 มิลลิเฮนรี

ตามสูตรการเชื่อมต่อแบบตรงกันข้าม

$\begin{align*} \begin{split} & L_e_q_. = L_1 + L_2 - 2M \\ & = 10 + 15 - 2(10) \\ & = 10 + 15 - 20 \\ & = 25 - 20 \\ & L_e_q_. = 5\,\,mH \end{split} \end{align*}$

ดังนั้น โดยใช้สมการ เราจะได้ความต้านทานเหนี่ยวนำที่เท่ากัน 5 มิลลิเฮนรีเมื่อมีการเชื่อมต่อแบบอนุกรมตรงข้าม

สูตรของอินดักเตอร์ที่เชื่อมต่อแบบขนาน

วิธีการเชื่อมต่ออินดักเตอร์แบบขนาน

สามารถเชื่อมต่ออินดักเตอร์สองตัวแบบขนานได้โดย

แรงดันไฟฟ้าที่เกิดจากอินดักเตอร์ช่วยเสริมแรงดันไฟฟ้าที่เกิดจากตนเอง คือ การเชื่อมต่อแบบขนานเสริม
แรงดันไฟฟ้าที่เกิดจากอินดักเตอร์ต้านทานแรงดันไฟฟ้าที่เกิดจากตนเอง คือ การเชื่อมต่อแบบขนานต้านทาน

การเชื่อมต่อแบบขนานเสริม (Cumulative) (แรงดันไฟฟ้าที่เกิดจากอินดักเตอร์ช่วยเสริมแรงดันไฟฟ้าที่เกิดจากตนเอง)

เมื่ออินดักเตอร์สองตัวถูกเชื่อมต่อแบบขนานเสริม แรงดันไฟฟ้าที่เกิดจากอินดักเตอร์จะช่วยเสริมแรงดันไฟฟ้าที่เกิดจากตนเอง เช่นในรูปภาพด้านล่าง

ให้ i₁ และ i₂ เป็นกระแสที่ไหลผ่านอินดักเตอร์ L₁ และ L₂ และ I เป็นกระแสรวม

ดังนั้น

(7) $\begin{equation*} i = i_1 + i_2 \end{equation*}$

ดังนั้น

(8) $\begin{equation*} \frac{di}{dt} = \frac{di_1}{dt} + \frac{di_2}{dt} \end{equation*}$

ในแต่ละอินดักเตอร์จะมีแรงดันไฟฟ้าสองชนิดที่ถูกเหนี่ยวนำขึ้น หนึ่งจากแรงดันไฟฟ้าที่เกิดจากตนเองและอีกหนึ่งจากแรงดันไฟฟ้าที่เกิดจากการเหนี่ยวนำร่วมกัน

เนื่องจากอินดักเตอร์เชื่อมต่อแบบขนาน แรงดันไฟฟ้าจึงเท่ากัน

ดังนั้น

(9) $\begin{equation*} L_1 \frac{di_1}{dt} + M \frac{di_2}{dt} = L_2 \frac{di_2}{dt} + M \frac{di_1}{dt} \end{equation*}$

$\begin{align*} L_1 \frac{di_1}{dt} - M \frac{di_1}{dt} = L_2 \frac{di_2}{dt} - M \frac{di_2}{dt} \end{align*}$

$\begin{align*} \frac{di_1}{dt} (L_1 - M) = \frac{di_2}{dt} (L_2 - M) \end{align*}$

(10) $\begin{equation*} \frac{di_1}{dt} = (\frac{L_2 - M}{L_1 - M}) \frac{di_2}{dt} \end{equation*}$

จากนั้น นำสมการ (9) มาแทนในสมการ (8) เราจะได้

$\begin{align*} \frac{di}{dt} = (\frac{L_2 - M}{L_1 - M}) \frac{di_2}{dt} + \frac{di_2}{dt} \end{align*}$

(11) $\begin{equation*} \frac{di}{dt} = (1 + \frac{L_2 - M}{L_1 - M}) + \frac{di_2}{dt} \end{equation*}$

ถ้า $L_e_q.$ เป็นอินดักแทนซ์ที่เทียบเท่าของอินดักเตอร์ที่เชื่อมต่อแบบขนาน แรงดันไฟฟ้าที่เกิดขึ้นในมันจะเป็น

(12) $\begin{equation*} e = L_e_q_. \frac{di}{dt} \end{equation*}$

นี่เท่ากับแรงดันไฟฟ้าที่เกิดขึ้นในวงจรขดลวดใดๆ คือ

$\begin{align*} L_e_q_. \frac{di}{dt} = L_1 \frac{di_1}{dt} + M \frac{di_2}{dt} \end{align*}$

(13) $\begin{equation*} \frac{di}{dt} = \frac{1}{L_e_q_.} [L_1 \frac{di_1}{dt} + M \frac{di_2}{dt}] \end{equation*}$

แทนค่าของ $\frac{di_1}{dt}$ จากสมการ (10) ลงในสมการ (13) เราจะได้

$\begin{align*} \frac{di}{dt} = \frac{1}{L_e_q_.} [L_1 (\frac{L_2 - M}{L_1 - M}) \frac{di_2}{dt} + M \frac{di_2}{dt}] \end{align*}$

(14) $\begin{equation*} \frac{di}{dt} = \frac{1}{L_e_q_.} [L_1 (\frac{L_2 - M}{L_1 - M}) + M] \frac{di_2}{dt} \end{equation*}$

ตอนนี้ ให้เทียบสมการ (11) กับสมการ (14)

$\begin{align*} 1+(\frac{L_2 - M}{L_1 - M}) \frac{di_2}{dt} = \frac{1}{L_e_q_.}[L_1 (\frac{L_2 - M}{L_1 - M}) + M]\frac{di_2}{dt} \end{align*}$

$\begin{align*} \frac{L_1+L_2 - 2M}{L_1 - M} = \frac{1}{L_e_q_.} [\frac{L_1L_2- L_1M+L_1M - M^2}{L_1 - M}] \end{align*}$

$\begin{align*} \frac{L_1+L_2 - 2M}{L_1 - M} = \frac{1}{L_e_q_.} [\frac{L_1L_2 - M^2}{L_1 - M}] \end{align*}$

(15) $\begin{equation*} L_e_q_. = \frac{L_1L_2 - M^2}{L_1+L_2 - 2M} \end{equation*}$

สมการดังกล่าวให้ค่าความต้านทานอินดักทีฟเทียบเท่าของสองอินดักทอร์ที่เชื่อมต่อแบบขนานช่วยหรือเชื่อมต่อแบบสะสม

หากไม่มีความต้านทานอินดักทีฟร่วมระหว่างวงจรสองวง (เช่น M = 0) แล้ว

$\begin{align*} L_e_q_. = \frac{L_1L_2 - (0)^2}{L_1+L_2-2(0)} = \frac{L_1L_2}{L_1+L_2} = \frac{product}{sum} \end{align*}$

การเชื่อมต่อแบบขนานตรงข้าม (Differential) (แรงดันไฟฟ้าที่เหนี่ยวนำร่วมกันต้านแรงดันไฟฟ้าที่เหนี่ยวนำเอง)

เมื่อสองอินดักเตอร์ถูกเชื่อมต่อแบบขนานตรงข้าม แรงดันไฟฟ้าที่เหนี่ยวนำร่วมกันจะต้านแรงดันไฟฟ้าที่เหนี่ยวนำเอง

ตามที่แสดงในภาพด้านล่าง สองอินดักเตอร์ถูกเชื่อมต่อแบบขนานตรงข้ามหรือแบบ Differential

ในทำนองเดียวกับการเชื่อมต่อแบบขนานช่วยเสริม สามารถพิสูจน์ได้ว่า

(16) $\begin{equation*} L_e_q_. = \frac{L_1L_2 - M^2}{L_1+L_2 + 2M} \end{equation*}$

สมการดังกล่าวให้ค่าความจุเหนี่ยวนำเทียบเท่าของสองอินดักเตอร์ที่เชื่อมต่อแบบขนานตรงข้ามหรือแบบ Differential

หากไม่มีความจุเหนี่ยวนำร่วมกันระหว่างสองคอยล์ (คือ M = 0) แล้ว

$\begin{align*} L_e_q_. = \frac{L_1L_2 - (0)^2}{L_1+L_2+2(0)} = \frac{L_1L_2}{L_1+L_2} = \frac{product}{sum} \end{align*}$

ตัวอย่างที่ 1

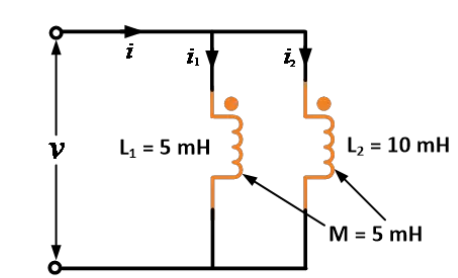
มีอินดักเตอร์สองตัวที่มีความเหนี่ยวนำต่อตัวเองเท่ากับ 5 มิลลิเฮนรีและ 10 มิลลิเฮนรี และความเหนี่ยวนำระหว่างกันเป็น 5 มิลลิเฮนรี หาค่าความเหนี่ยวนำที่เทียบเท่าเมื่อมีการเชื่อมต่อแบบขนานช่วยกัน

วิธีทำ:

ข้อมูลที่ให้มา: L₁ = 5 มิลลิเฮนรี, L₂ = 10 มิลลิเฮนรี และ M = 5 มิลลิเฮนรี

ตามสูตรของการเชื่อมต่อแบบขนานช่วยกัน

$\begin{align*} \begin{split} & L_e_q_. = \frac{L_1 L_2 - M^2}{L_1 + L_2 - 2M}.... if \,\, fluxes \,\, aid \\ & = \frac{5 * 10 - (5)^2}{5 + 10 - 2(5)} \\ & = \frac{50 - 25}{15 - 10} \\ & = \frac{25}{5} \\ & L_e_q_. = 5\,\,mH \end{split} \end{align*}$

ดังนั้น โดยใช้สมการ เราจะได้ค่าความเหนี่ยวนำที่เทียบเท่าเท่ากับ 5 มิลลิเฮนรี เมื่อมีการเชื่อมต่อแบบขนานช่วยกัน

ตัวอย่างที่ 2

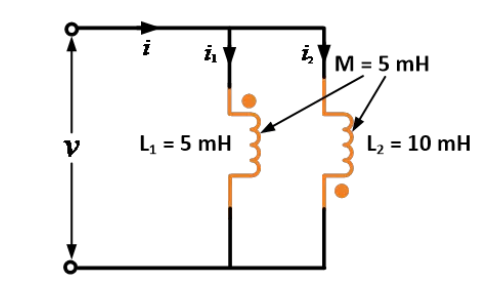
ตัวเหนี่ยวนำสองตัวมีค่าอินดักแทนซ์ของตัวเองเป็น 5 mH และ 10 mH โดยมีมิวชวลอินดักแทนซ์ระหว่างกันเท่ากับ 5 mH จงหาค่าอินดักแทนซ์รวมเมื่อเชื่อมต่อแบบขนานในลักษณะที่สนามแม่เหลือขัดขวางกัน

วิธีทำ:

ข้อมูลที่กำหนดให้: L1 = 5 mH, L2 = 10 mH และ M = 5 mH

ตามสูตรการเชื่อมต่อแบบขนานที่สนามขัดขวางกัน

$\begin{align*} \begin{split} & L_e_q_. = \frac{L_1 L_2 - M^2}{L_1 + L_2 + 2M}.... if \,\, fluxes \,\, oppose \\ & = \frac{5 * 10 - (5)^2}{5 + 10 + 2(5)} \\ & = \frac{50 - 25}{15 + 10} \\ & = \frac{25}{25} \\ & L_e_q_. = 1\,\,mH \end{split} \end{align*}$

ดังนั้น เมื่อใช้สมการ เราจะได้ค่าอินดักแทนซ์รวมเท่ากับ 1 mH เมื่อเชื่อมต่อแบบขนานในลักษณะที่สนามแม่เหลือขัดขวางกัน

Coupling Inductors

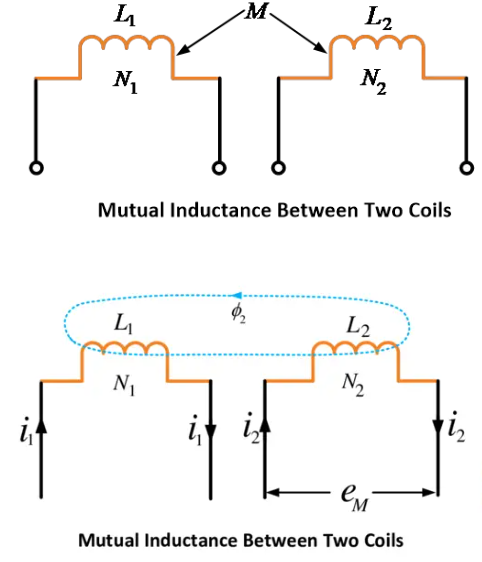
เมื่อสนามแม่เหล็กของตัวเหนี่ยวนำหนึ่ง (คอยล์) ตัดหรือเชื่อมโยงกับขดลวดของตัวเหนี่ยวนำอีกตัวหนึ่งที่อยู่ใกล้เคียง ตัวเหนี่ยวนำทั้งสองนี้จะถือว่าถูกผูกพันทางแม่เหล็กกัน ซึ่งจากการผูกพันนี้ จะทำให้เกิดมิวชวลอินดักแทนซ์ระหว่างคอยล์ทั้งสอง

ในวงจรที่ถูกผูกพันกัน การถ่ายโอนพลังงานจะเกิดขึ้นจากวงจรหนึ่งไปยังอีกวงจรหนึ่งเมื่อมีการจ่ายพลังงานให้กับวงจรใดวงจรหนึ่ง เช่น หม้อแปลงไฟฟ้าแบบสองขดลวด หม้อแปลงอัตโนมัติ และ มอเตอร์เหนี่ยวนำ เป็นตัวอย่างของตัวเหนี่ยวนำหรือคอยล์ หรือวงจรที่ถูกผูกพันทางแม่เหล็กกัน

พิจารณาอินดักเตอร์หรือขดลวดที่มีการเชื่อมโยงทางแม่เหล็ก 1 และ 2 ซึ่งมีความเหนี่ยวนำ L1 และ L2 ตามลำดับ ให้ M เป็นความเหนี่ยวนำร่วมระหว่างขดลวดทั้งสอง

ผลของความเหนี่ยวนำร่วมคือเพิ่ม (L1 + M และ L2 + M) หรือลด (L1 – M และ L2 – M) ความเหนี่ยวนำของขดลวดทั้งสอง ขึ้นอยู่กับการจัดเรียงของขดลวดหรืออินดักเตอร์ทั้งสอง

เมื่อขดลวดทั้งสองถูกจัดเรียงให้ฟลักซ์ของพวกมันช่วยเสริมกัน ความเหนี่ยวนำของแต่ละขดลวดจะเพิ่มขึ้นโดย M คือ มันกลายเป็น L1 + M สำหรับขดลวด 1 และ L2 + M สำหรับขดลวด 2 เนื่องจากฟลักซ์รวมที่เชื่อมโยงกับแต่ละขดลวดมากกว่าฟลักซ์ของตัวเอง
เมื่อขดลวดทั้งสองถูกจัดเรียงให้ฟลักซ์ของพวกมันตรงข้ามกัน ความเหนี่ยวนำของแต่ละขดลวดจะลดลงโดย M คือ มันกลายเป็น L1 – M สำหรับขดลวด 1 และ L2 – M สำหรับขดลวด 2 เนื่องจากฟลักซ์รวมที่เชื่อมโยงกับแต่ละขดลวดน้อยกว่าฟลักซ์ของตัวเอง

สูตรความเหนี่ยวนำร่วม

เราทราบว่าการเปลี่ยนแปลงกระแสในขดลวดหนึ่งจะทำให้เกิดแรงดันไฟฟ้าที่เหนี่ยวนำแบบร่วมในขดลวดที่สองเสมอ

ความเหนี่ยวนำร่วมถูกกำหนดว่าเป็นความสามารถของขดลวดหนึ่ง (หรือวงจร) ในการสร้างแรงดันไฟฟ้าที่เหนี่ยวนำในขดลวดใกล้เคียง (หรือวงจร) โดยการเหนี่ยวนำเมื่อกระแสในขดลวดแรกเปลี่ยนแปลง

กล่าวอีกนัยหนึ่ง คุณสมบัติของขดลวดสองขดที่ทำให้แต่ละขดต่อต้านการเปลี่ยนแปลงของกระแสที่ไหลผ่านขดลวดอื่นเรียกว่าความเหนี่ยวนำร่วมระหว่างขดลวดทั้งสอง การต่อต้านนี้เกิดขึ้นเนื่องจากการเปลี่ยนแปลงของกระแสในขดลวดหนึ่งทำให้เกิดแรงดันไฟฟ้าที่เหนี่ยวนำแบบร่วมในขดลวดอื่นซึ่งต่อต้านการเปลี่ยนแปลงของกระแสในขดลวดแรก

ความเหนี่ยวนำร่วม (M) อาจถูกกำหนดว่าเป็นฟลักซ์ที่เชื่อมโยงกับขดลวดต่อหน่วยกระแสในขดลวดอื่น

ทางคณิตศาสตร์

$\begin{align*} M = \frac{N_2 \phi_1_2}{I_1} \end{align*}$

ที่,

$I_1$ = กระแสไฟฟ้าในขดลวดแรก

$\phi_1_2$ = ฟลักซ์ที่เชื่อมโยงกับขดลวดที่สอง

$N_2$ = จำนวนรอบของขดลวดที่สอง

ความเหนี่ยวนำร่วมระหว่างขดลวดสองขดเป็น 1 เฮนรี ถ้ากระแสเปลี่ยนแปลงที่อัตรา 1 แอมแปร์ต่อวินาทีในขดลวดหนึ่งทำให้เกิดแรงดันไฟฟ้า 1 V ในขดลวดอื่น ๆ

สัมประสิทธิ์การเชื่อมโยง

สัมประสิทธิ์การเชื่อมโยง (k) ระหว่างขดลวดสองขดกำหนดโดยเป็นเศษส่วนของ ฟลักซ์แม่เหล็ก ที่ผลิตโดยกระแสในขดลวดหนึ่งที่เชื่อมโยงกับขดลวดอื่น ๆ

สัมประสิทธิ์การคู่เป็นพารามิเตอร์ที่สำคัญสำหรับวงจรที่เชื่อมต่อกันเพื่อกำหนดปริมาณการคู่ระหว่างขดลวดที่เชื่อมต่อแบบเหนี่ยวนำ

ทางคณิตศาสตร์ สัมประสิทธิ์การคู่สามารถแสดงได้ว่า

$\begin{align*} k = \frac{M}{\sqrt{L_1L_2}} \end{align*}$

โดยที่

L1 คือความเหนี่ยวนำของตนเองของขดลวดแรก

L2 คือความเหนี่ยวนำของตนเองของขดลวดที่สอง

M คือความเหนี่ยวนำร่วมระหว่างสองขดลวด

สัมประสิทธิ์การคู่ขึ้นอยู่กับความเหนี่ยวนำร่วมระหว่างสองขดลวด หากสัมประสิทธิ์การคู่สูง ความเหนี่ยวนำร่วมก็จะสูงตามไปด้วย สองขดลวดที่เชื่อมต่อแบบเหนี่ยวนำจะเชื่อมโยงกันผ่านฟลักซ์แม่เหล็ก

เมื่อฟลักซ์ทั้งหมดของขดลวดหนึ่งเชื่อมโยงกับขดลวดอื่น สัมประสิทธิ์การคู่จะเท่ากับ 1 (คือ 100%) แล้วขดลวดถูกเรียกว่าเชื่อมต่อแน่น
หากฟลักซ์ที่สร้างขึ้นในขดลวดหนึ่งเชื่อมโยงกับขดลวดอื่นเพียงครึ่งหนึ่ง สัมประสิทธิ์การคู่จะเท่ากับ 0.5 (คือ 50%) แล้วขดลวดถูกเรียกว่าเชื่อมต่อหลวม
หากฟลักซ์ของขดลวดหนึ่งไม่เชื่อมโยงกับขดลวดอื่นเลย สัมประสิทธิ์การคู่จะเท่ากับ 0 ขดลวดถูกเรียกว่าแยกจากกันทางแม่เหล็ก

สัมประสิทธิ์การคู่จะมีค่าน้อยกว่า 1 เสมอ ขึ้นอยู่กับวัสดุที่ใช้ทำแกน สำหรับแกนอากาศ สัมประสิทธิ์การคู่อาจอยู่ระหว่าง 0.4 ถึง 0.8 ขึ้นอยู่กับระยะห่างระหว่างสองขดลวด และสำหรับแกนเหล็กหรือเฟอร์ไรต์ อาจสูงถึง 0.99

แหล่งที่มา: Electrical4u.

คำชี้แจง: ให้ความเคารพต่องานเขียนเดิม บทความที่ดีควรแบ่งปัน หากมีการละเมิดลิขสิทธิ์โปรดติดต่อเพื่อลบ