මීට කියන්නේ මාරුකාඩුවෙන් කියන්නේ ඇයි?
මාරුකාඩුව (මහාවිද්යුත් මාරුකාඩුව ලෙසද හැඳින්විය හැක) යනු දෙක් පිටි ඇති පාසිව් මහාවිද්යුත් මූලද්රව්යය නම් මූලද්රව්යයක් ලෙස නිර්ණය කරනු ලබන අතර එය රැගෙන යන්නේ මාග්නෑටික ක්ෂේත්රයේ ආකෘතියක් ලෙස ශක්තිය ගබඩා කිරීමයි. එයට විද්යුත් ධාරාව ටොක්කෝ පැවැත්විය යුතුය. එය මූලිකාවේදී කෝයිල්, චොක්ස් හෝ රියැක්ටරයක් ලෙසද හැඳින්විය හැකිය.
මාරුකාඩුව යනු සරලවම ගැටුමක් මූලද්රව්යයකි. එය නියමයෙන්ම ගැටුමක් ලෙස පිළිගැනීමේ උපකරණයක් ලෙස භාවිතා කරනු ලබන විදියට බැඳුනු තිත් පිටියක් ලෙස සැලකිය හැකිය, එය සාමාන්යයෙන්ම බෙදීම් තිත් පිටියක්, බෙදීම් තිත් පිටියක් ලෙස භාවිතා කරනු ලබන අතර, එය ප්ලාස්ටික් හෝ ෆෙරෝමාග්නෑටික මූලද්රව්යයක් ලෙස බැඳුනු ඉරි පිටියක් ලෙස සැලකිය හැකිය; එය ඉරි පිටි මාරුකාඩුව ලෙස හැඳින්විය හැකිය.
මාරුකාඩුවන් යනු නියමයෙන්ම 1 µH (10-6 H) සිට 20 H ට පමණ පරාසයක් තුළ ලබා දී ඇත. බොහෝ මාරුකාඩුවන්ට ගැටුමක් තුළ පිහිටුනු ප්ලාස්ටික් හෝ ඉරි පිටියක් ඇති අතර, එය භාවිතා කරනු ලබන්නේ මාග්නෑටික ක්ෂේත්රය සහ එයට අනුව මාරුකාඩුවේ මාරුකාඩු බලය වැඩි කිරීම සඳහාය.
ෆැරඩියේ ප්රතිමානික ප්රාව්ර්ත්ය නියමයට අනුව, මාරුකාඩුවකට හෝ කෝයිල් එකකට ටොක්කෝ පැවැත්විය යුතු විද්යුත් ධාරාව වෙනස් වූ විට, කාලය වෙනස් වන මාග්නෑටික ක්ෂේත්රය එකකට e.m.f (ක්රියාකාරී බලය) හෝ විශ්කමිතාව ඇතුලත් කරනු ලබන්නේය. මාරුකාඩුවකට ඇතුලත් කරනු ලබන e.m.f. හෝ විශ්කමිතාව ටොක්කෝ පැවැත්විය යුතු විද්යුත් ධාරාවේ වෙනස් වීමේ අනුපාතයට සෘණීය වේ.
ඉන්ඩක්ටන්ස් (L) යනු එය හරහා ගලා යන ධාරාවේ ප්රමාණය හෝ දිශාව වෙනස් වීමට එරෙහිව ක්රියා කරන ඉන්ඩක්ටරයක ගුණයකි. ඉන්ඩක්ටරයක ඉන්ඩක්ටන්ස් වැඩි වන තරමට, චුම්බක ක්ෂේත්රයක් ලෙස විදුලි ශක්තිය ගබඩා කර ගැනීමේ හැකියාව ද වැඩි වේ.
ඉන්ඩක්ටර් ක්රියා කරන්නේ කෙසේද?
පරිපථයක ඇති ඉන්ඩක්ටරය ධාරා ප්රවාහයේ වෙනස්වීමට එරෙහිව ක්රියා කරන්නේ එහි අවසානයේ වෝල්ටීයතාවක් උත්පාදනය කිරීම මගිනි. මෙම වෝල්ටීයතාව ධාරා ප්රවාහයේ වෙනස්වීමේ සීඝ්රතාවයට සමානුපාතික වේ. පරිපථයක ඉන්ඩක්ටරය ක්රියා කරන ආකාරය තේරුම් ගැනීම සඳහා, පහත දැක්වෙන රූපය සලකා බලන්න.
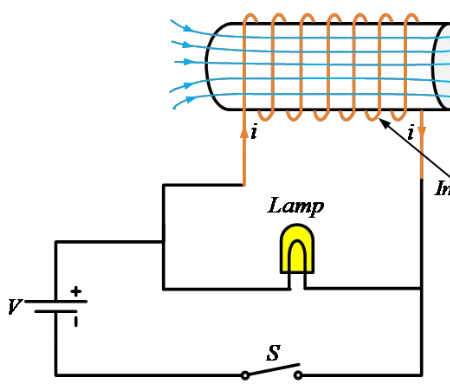 පරිපථයක ඉන්ඩක්ටරය ක්රියා කිරීම
පරිපථයක ඉන්ඩක්ටරය ක්රියා කිරීම
ඉහත දැක්වෙන පරිදි, බැටරියක් සමඟ ලාම්පුවක්, වයර් කුණ්ඩයක් (ඉන්ඩක්ටරය), සහ ස්විචයක් සම්බන්ධ කර ඇත. අපි පරිපථයෙන් ඉන්ඩක්ටරය ඉවත් කරන්නේ නම්, ලාම්පුව සාමාන්ය ලෙස දීප්තිමත් වේ. ඉන්ඩක්ටරය සමඟ, පරිපථය සම්පූර්ණයෙන්ම වෙනස් ලෙස ආචරණය කරයි.
ඉන්ඩක්ටරය හෝ කුණ්ඩය ලාම්පුව සමඟ සැසඳූ විට බෙහෙවින් අඩු ප්රතිරෝධයක් ඇති අතර, එබැවින් ස්විචය වැසූ විට ධාරාවට අඩු ප්රතිරෝධක මාර්ගයක් සැපයීම නිසා බොහෝ ධාරාව කුණ්ඩය හරහා ගලා යා යුතුය. එබැවින්, ලාම්පුව ඉතා අඩුවෙන් දීප්තිමත් වනු අප බලාපොරොත්තු විය හැකිය.
නමුත් පරිපථයේ ඉන්ඩක්ටරයේ ආචරණය නිසා, අපි ස්විචය වැසූ විට, ලාම්පුව තියුණුව දීප්තිමත් වන අතර පසුව අඳුරු වන අතර, ස්විචය විවෘත කළ විට, බල්බය ඉතා තියුණුව දීප්තිමත් වන අතර ඉක්මනින් අඳුරු වේ.
හේතුව නම්, ඉන්ඩක්ටරයකට ප්රතිවිරුද්ධතාවක් හෝ වෝල්ටීයතාවක් අදිශ වූ විට, ඉන්ඩක්ටරය හරහා ගලා යන විදුලි ධාරාව චුම්බක ක්ෂේත්රයක් නිපදවයි. මෙම චුම්බක ක්ෂේත්රය නැවත ඉන්ඩක්ටරයේ ආවේශිත විදුලි ධාරාවක් නිපදවයි, නමුත් ලෙන්ස් නියමයට අනුව එය විරුද්ධ ධ්රැවකතාවක් ඇත.
ඉන්ඩක්ටරයේ චුම්බක ක්ෂේත්රය නිසා ඇතිවන මෙම ආවේශිත ධාරාව වැඩිවීමක් හෝ අඩුවීමක් වැනි ඕනෑම වෙනසක් වෙත එරෙහිව ක්රියා කිරීමට උත්සාහ කරයි. චුම්බක ක්ෂේත්රය ගොඩනැගුණු පසු, ධාරාව සාමාන්ය ලෙස ගලා යා හැකිය.
දැන්, ස්විචය වැසූ විට, ඉන්ඩක්ටරය වටා ඇති චුම්බක ක්ෂේත්රය ඉන්ඩක්ටරයේ ධාරාව ගලා යාම පවත්වා ගන්නා අතර චුම්බක ක්ෂේත්රය කඩා වැටෙන තෙක්ම එය පවතී. මෙම ධාරාව ස්විචය විවෘත වුවද ලාම්පුව නිශ්චිත කාලයක් දීප්තිමත් වීමට පවත්වා ගනී.
වෙනත් අයුරු කිවහොත්, ඉන්ඩක්ටරය චුම්බක ක්ෂේත්රයක් ලෙස ශක්තිය ගබඩා කර ගත හැකි අතර, එය එහි හරහා ගලා යන ධාරාවේ ඕනෑම වෙනසක් වෙත එරෙහිව ක්රියා කිරීමට උත්සාහ කරයි. එබැවින්, මෙයින් ප්රතිඵලයක් ලෙස, ඉන්ඩක්ටරයක් හරහා ධාරාව අක්ෂරාර්ථයෙන් වෙනස් විය නොහැක.
ඉන්ඩක්ටර් පරිපථ සංකේතය
ඉන්ඩක්ටරයක සිතියම් පරිපථ සංකේතය පහත දැක්වෙන රූපයේ දැක්වේ.
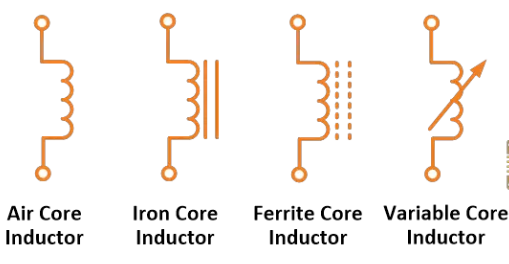
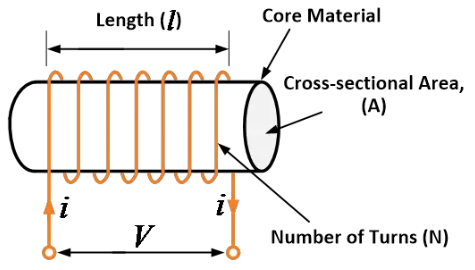 ඇඩක්ටරයේ සංකේතය
ඇඩක්ටරයේ සංකේතය
ඇඩක්ටර සමීකරණය
ඇඩක්ටරයේ උත්පන්න ධාරාව
ඇඩක්ටරයේ උත්පන්න ධාරාව එහිදී පැවතෙන රෝග්ස් ධාරාවේ ප්රතිස්ථාපනයට සමානුපාතිකයි. ගණිතමයව, ඇඩක්ටරයේ උත්පන්න ධාරාව පහත ආකාරයේ ලියනු ලබනු ලැබේ,

යන්නේ, = ඇඩක්ටරයේ තුල මිලීවින්ට් ප්රමාණයේ දිගින් පිළිගැනීම,
= ඇඩක්ටරයේ තුල මිලීවින්ට් ප්රමාණයේ දිගින් පිළිගැනීම,
 = හෙන්රි ප්රමාණයේ ඇඩක්ටර,
= හෙන්රි ප්රමාණයේ ඇඩක්ටර,
 = ටෙස්ලා ප්රමාණයේ විස්තාරයේ ප්රතිස්ථාපනය
= ටෙස්ලා ප්රමාණයේ විස්තාරයේ ප්රතිස්ථාපනය
කුලියට අතර වූ විද්යුත් තාවකය කුලියේ උත්සාහ ක්ෂේත්රයේ පිළිබඳ ගබඩා කරන ආකාරයෙන් ලැබේ.
මීට පසු ගැලපෙන ධාරාව කුලිය තුළ ගමන් කරන විට  කාලයට පිළිබඳව නියත වන බැවින් ශුන්ය වේ. මෙය නිසා, කුලිය තුළ විද්යුත් තාවකය ශුන්ය වේ. මෙන්නෑ, ගැලපෙන ධාරා පිළිබඳ පිළිබඳ අවස්ථාවේ, කුලිය නියත පිළිබඳ රැයක් ලෙස ක්රියා කරයි.
කාලයට පිළිබඳව නියත වන බැවින් ශුන්ය වේ. මෙය නිසා, කුලිය තුළ විද්යුත් තාවකය ශුන්ය වේ. මෙන්නෑ, ගැලපෙන ධාරා පිළිබඳ පිළිබඳ අවස්ථාවේ, කුලිය නියත පිළිබඳ රැයක් ලෙස ක්රියා කරයි.
කුලිය තුළ ධාරාව
කුලිය තුළ ධාරාව පහත දැක්වූ ආකාරයෙන් විද්යුත් තාවකය පිළිබඳ ලෙස පිළිවෙලින් පිළිබඳ කළ හැකිය

මෙම සමීකරණයේ අනුකලනයේ සීමා පැවැත්වීම අතීත ඉතිහාසය හෝ ප්රാරම්භික පරිදි බලා දී ඇත, එනම්  යන පරිදි.
යන පරිදි.
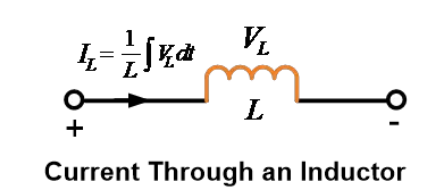
දැන්, t=0 ට නියැළි ක්රියා සිදු වන බව උපකල්පනය කරන්න, එනම් t=0 ට නියැළිය සොයා ගෙන ඇත. අපට කුලිය තුළ ධාරාව සඳහා සමීකරණයක් ලැබේ,

නියත පරාස දෙකට බෙදීමේ සීමාවන්  සහ
සහ  ලෙස බෙදිය හැකිය. අපි
ලෙස බෙදිය හැකිය. අපි  යනු වෙනස් කිරීම සිදු වන තුරු පෙර මූලික තුළින් පිළිබඳ වශයෙන් දැනගැනීමට ලැබේ, එනම්
යනු වෙනස් කිරීම සිදු වන තුරු පෙර මූලික තුළින් පිළිබඳ වශයෙන් දැනගැනීමට ලැබේ, එනම්  යනු වෙනස් කිරීම සිදු වන පසු මූලික තුළින් පිළිබඳ වශයෙන් දැනගැනීමට ලැබේ. එබැවින්, අපි පහත ආකාරයට ලියා දැක්විය හැකිය
යනු වෙනස් කිරීම සිදු වන පසු මූලික තුළින් පිළිබඳ වශයෙන් දැනගැනීමට ලැබේ. එබැවින්, අපි පහත ආකාරයට ලියා දැක්විය හැකිය

එබැවින්,

මෙහි,  යන්න පැවැත්වෙන්නේ අතීතයේ තුළ ප්රදේශ විද්යුත් ධාරාවේ අගය පිළිබඳවයි, එය නිසා
යන්න පැවැත්වෙන්නේ අතීතයේ තුළ ප්රදේශ විද්යුත් ධාරාවේ අගය පිළිබඳවයි, එය නිසා  මූලික අවස්ථාවයි. එයට
මූලික අවස්ථාවයි. එයට  කියා සංකේත කළ හැකිය.
කියා සංකේත කළ හැකිය.

විට,  ලෙස ලියන්න හැකිය,
ලෙස ලියන්න හැකිය,

මෙහිදී අපි සැකසුම් ක්රියාව වශයෙන් සිදුවන්නේ කාලය විසින් අර්ථ දැක්වීමට පෙර මෙහිදී උපක්රමණය කළා. එබැවින්,  සිට
සිට  ට ගෙන යන අනුකලනය වශයෙන් අගය ශුන්යයි.
ට ගෙන යන අනුකලනය වශයෙන් අගය ශුන්යයි.
එබැවින්,

එබැවින්, තුඩුවේ තීරණය වෙනස් කිරීම නියත කාලයක් තුළ සිදු විය නොහැක. එය අර්ථ කරනුයේ, තුඩුවේ තීරණය, සැකසුම් ක්රියාව පෙර සහ පසු සමාන වේ.
t=0 විට තුඩුව
අනුක්මනය  , එනම්, අනුක්මනය පරිවර්තනය කිරීමේ විට, අනුක්මනය පාදය තුළ ප්රතිඵලය නිදහස්ව යුතු ලෙස
, එනම්, අනුක්මනය පරිවර්තනය කිරීමේ විට, අනුක්මනය පාදය තුළ ප්රතිඵලය නිදහස්ව යුතු ලෙස  පැවතී, දේසීය කාලය
පැවතී, දේසීය කාලය  ශූන්ය වන බැවිනි. මෙම නිසා, පරිවර්තන කිරීමේ විට අනුක්මනය පාදය උදෑසීමක් ලෙස ක්රියා කරයි. එහෙත්,
ශූන්ය වන බැවිනි. මෙම නිසා, පරිවර්තන කිරීමේ විට අනුක්මනය පාදය උදෑසීමක් ලෙස ක්රියා කරයි. එහෙත්,  පැවැත්විය යුතු ප්රකාශයේදී, එය ප්රතිඵලයක් ලෙස ක්රියා කරයි.
පැවැත්විය යුතු ප්රකාශයේදී, එය ප්රතිඵලයක් ලෙස ක්රියා කරයි.
යම් අනුක්මනයක් පරිවර්තන කිරීමට පෙර I0 ප්රാരംഭ ධාරාවක් ගෙන ඇත්නම්, එවක  පිළිවෙලින්, එය
පිළිවෙලින්, එය  අගයක් ප්රතිඵලයක් ලෙස ක්රියා කරයි, එහෙත්,
අගයක් ප්රතිඵලයක් ලෙස ක්රියා කරයි, එහෙත්,  පැවැත්විය යුතු ප්රකාශයේදී, එය ප්රතිඵලයක් ලෙස ක්රියා කරයි.
පැවැත්විය යුතු ප්රකාශයේදී, එය ප්රතිඵලයක් ලෙස ක්රියා කරයි.
ආපසු සහ පරාල්ල අනුක්මනයන්
සේරියාගේ හා පැරල්ලේ ඉන්ඩක්ටර් යනුවෙන් දී ඇති ලෙස රිසිස්ටර් සේරියාගේ හා පැරල්ලේ ආචරණය කරනු ලබනු උදාහරණ මාර්ගයකි. එක් එක් මාග්නෑටික වශයෙන් සම්බන්ධ කොයිල් 1 සහ 2 සහිත ස්ව-ඉන්ඩක්ටන්ස්  සහ
සහ  එක් එක් නිරූපණය කරනු ලබනු උදාහරණ මාර්ගයකි. M යනු ශ්රි ප්රමාණයේ යුගල කොයිල් අතර මුතු ඉන්ඩක්ටන්ස් යි.
එක් එක් නිරූපණය කරනු ලබනු උදාහරණ මාර්ගයකි. M යනු ශ්රි ප්රමාණයේ යුගල කොයිල් අතර මුතු ඉන්ඩක්ටන්ස් යි.
විද්යුත් චක්රයක් විසින් ඇති ඉන්ඩක්ටර් යුගල විවිධ ආකාරයෙන් සම්බන්ධ කළ හැකි අතර එය තවත් සම්බන්ධ කිරීමේ ප්රමාණයක් ලබා දෙයි.
සේරියාගේ ඉන්ඩක්ටර් සූත්රය
සේරියාගේ ඉන්ඩක්ටර් එකතු කිරීමේ ක්රමය
දැන් පැරල්ලේ සම්බන්ධ කළ ඇති යුගල ඉන්ඩක්ටර් හෝ කොයිල් යුගල අන්තර්ගත වූ චක්රයක් සැලකීම. මෙය සේරියාගේ ඉන්ඩක්ටර් එකතු කිරීමේ ප්රමාණයක් ලබා දෙයි.
පළමු ක්රමයේ, ඉන්ඩක්ටර් යුගල විසින් ඇති ස්ප්රොත් ප්රවාහයන් එකම දිශාවට ක්රියා කරනු ලබනු උදාහරණ මාර්ගයකි. එවිට, එම ඉන්ඩක්ටර් යුගල සේරියාගේ-උපකාරක හෝ බෙදීමේ ප්රකාරයෙන් සම්බන්ධ කළ ඇති ලෙස කියනු ලැබේ.
දෙවැනි ක්රමයේ, ඉන්ඩක්ටර් යුගල එක්කේ ප්රතිවිරුද්ධ ප්රවාහය ඇති නම්, ඉන්ඩක්ටර් විසින් ඇති ස්ප්රොත් ප්රවාහයන් එකිනෙකට ප්රතිවිරුද්ධ ක්රියා කරනු ලබනු උදාහරණ මාර්ගයකි. එවිට, එම ඉන්ඩක්ටර් යුගල සේරියාගේ-ප්රතිවිරුද්ධ හෝ බෙදීමේ ප්රකාරයෙන් සම්බන්ධ කළ ඇති ලෙස කියනු ලැබේ.
මීටරය 1 වෙතින් එක් කළ ආසන්න ධාරාවේ යම් ප්රමාණයක් ලෙස  සහ මීටරය 2 වෙතින් එක් කළ ආසන්න ධාරාවේ යම් ප්රමාණයක් ලෙස
සහ මීටරය 2 වෙතින් එක් කළ ආසන්න ධාරාවේ යම් ප්රමාණයක් ලෙස  ලෙස නිරූපණය කරමු. එක් කළ පාදයන් දෙකම අන්තර්ගත ආසන්නතාව M විසින් එක්කර ඇත.
ලෙස නිරූපණය කරමු. එක් කළ පාදයන් දෙකම අන්තර්ගත ආසන්නතාව M විසින් එක්කර ඇත.
සේරියා උද්ධාරක (සමුචිත) සම්බන්ධතාව (අන්තර්ගතව උද්ධාරක ගති බලය එක් කළ ආසන්න ධාරාවේ EMF වලට උද්ධාරක වේ)
පහත දැක්වෙන ආකාරයට පාදයන් දෙකම සේරියා උද්ධාරක හෝ සමුචිතව එක්කර ඇත.
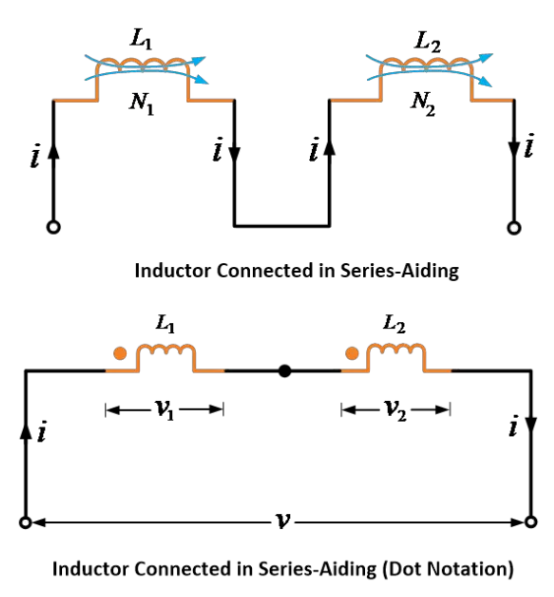
මෙම සම්බන්ධතාවේදී, පාදයන් දෙකම එක්කර ඇති ආසන්න ධාරාවේ සහ අන්තර්ගත ධාරාවේ ශ්රිත එක් ප්රදේශයේදී ක්රියා කරන අතර; එම නිසා එක්කර ඇති ආසන්න ධාරාවේ සහ අන්තර්ගතව උද්ධාරක ගති බල එක් ප්රදේශයේදී ක්රියා කරනු ලැබේ.
එබැවින්,
පාදය 1 එක්කර ඇති ආසන්න ධාරාවේ e.m.f., 
පාදය 1 අන්තර්ගතව උද්ධාරක ගති බල, 
පාදය 2 එක්කර ඇති ආසන්න ධාරාවේ e.m.f., 
ආයින්දු ප්රතික්රියාවක් සහිත ප්රථම ප්රස්තාරයේ උත්පාදිත ඉලෙක්ට්රොමොටීවික ක්රියාකාරීත්වය, 
සංයුක්ත ප්රස්තාරයේ උත්පාදිත මුළු ඉලෙක්ට්රොමොටීවික ක්රියාකාරීත්වය,

(1) 
යद්  ගණිතමය ප්රස්තාර දෙකක විශේෂ ප්රස්තාර ලෙස ප්රකාශ කෙරේ නම්, සංයුක්ත ප්රස්තාරයේ උත්පාදිත ඉලෙක්ට්රොමොටීවික ක්රියාකාරීත්වය පහත පරිදි ලෙස ලබා දැයි කියනු ලැබේ,
ගණිතමය ප්රස්තාර දෙකක විශේෂ ප්රස්තාර ලෙස ප්රකාශ කෙරේ නම්, සංයුක්ත ප්රස්තාරයේ උත්පාදිත ඉලෙක්ට්රොමොටීවික ක්රියාකාරීත්වය පහත පරිදි ලෙස ලබා දැයි කියනු ලැබේ,
(2) 
සමීකරණ (1) සහ (2) හි උපේක්ෂණය කිරීමෙන්,
(3) 
මෙම සමීකරණය දෙක් පිළිගැනීමේ හෝ එකතු කිරීමේ ශ්රේණියේ ප්රතිස්ථාපන උණුසු හෝ නිව්වීම් අතර සමාන උණුසු ගැලපෙන්නේ.
දෙක් නිව්වීම් අතර එක්සත් උණුසු නැතිනම් (ඉතින්, M = 0), නම්,

සේරිය නිර්වාරණය (අන්තර්ගත යාම) සම්බන්ධය (මූත්මිය ආර්ය මගින් ඇති ප්රතිඵලය ස්වාධීන උණුසු බල නිර්වාරණය කරයි
හැකි පරිදි දෙක් නිව්වීම් අතර එක්සත් උණුසු ඇති ප්රතිඵලයක් ඇති ලෙස සේරිය සම්බන්ධයට ඇතුලත් කරන ලද ප්රත්යාගාමී රේඛාවක් සැලකිය හැකිය, එහිදී දෙක් නිව්වීම් අතර භූමික එකතුවේ බල එකතුවට ප්රතික්රියා කරයි, පහත දැක්වෙන රූපයේ පරිදි.
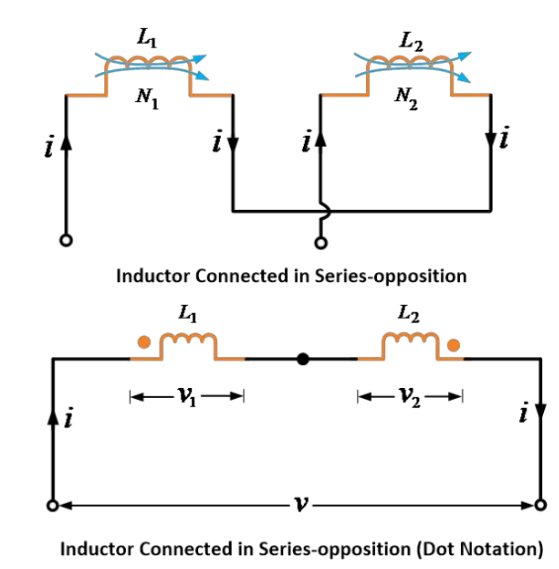
භූමික එකතුවේ බල එකතුවට ප්රතික්රියා කරන බැවින්, එක්සත් උණුසු ආර්ය මගින් ඇති ප්රතිඵලයේ ලකුණ ස්වාධීන උණුසු බල ලකුණට ප්රතික්රියා කරයි. නම්,
නිව්වීම් 1 තුළ ස්වාධීන උණුසු ආර්ය, 
ඉන්ඩක්ටරය 1 තුළ පරස්පරව උත්පාදිත e.m.f., 
ඉන්ඩක්ටරය 2 තුළ ස්වයං උත්පාදිත e.m.f., 
ඉන්ඩක්ටරය 1 තුළ පරස්පරව උත්පාදිත e.m.f., 
සංයෝජනය තුළ මුළු උත්පාදිත e.m.f.,

(4) 
If  ශ්රේණි ප්රතිවිරුද්ධ සම්බන්ධතාවක ඇති කුලකයක සමතුලිත ප්රේරණය නම්, සංයෝජනය තුළ උත්පාදිත e.m.f. ලබා දෙනු ලැබේ,
ශ්රේණි ප්රතිවිරුද්ධ සම්බන්ධතාවක ඇති කුලකයක සමතුලිත ප්රේරණය නම්, සංයෝජනය තුළ උත්පාදිත e.m.f. ලබා දෙනු ලැබේ,
(5) 
සමීකරණ (4) සහ (5) සංසන්දනය කිරීමෙන්, අපට ලැබේ,
(6) 
ඉහත සමීකරණය ශ්රේණි විරුද්ධතාවයේ හෝ වෙනස් සම්බන්ධතාවයේ සම්බන්ධ කර ඇති දෙකොපමණක සමතුලිත ප්රේරණය ලබා දෙයි.
කුඩා දෙකක් අතර අන්යෝන්ය ප්රේරණයක් නොමැති නම් (එනම්, M = 0), එවිට,

උදාහරණය 1
කුඩා දෙකක් 10 mH සහ 15 mH ස්වයං ප්රේරණයන් සහිතව ඇති අතර, ඒවා අතර අන්යෝන්ය ප්රේරණය 10 mH කි. ඒවා ශ්රේණි පෝෂණයේ සම්බන්ධ කර ඇති විට සමතුලිත ප්රේරණය සොයන්න.
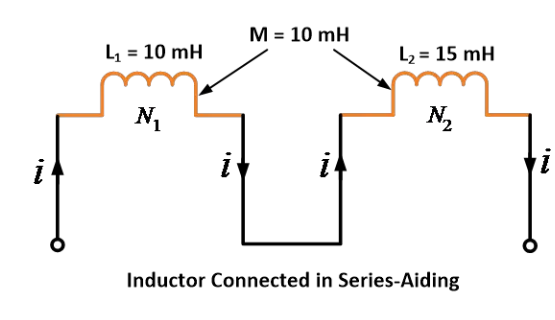
පිළිතුර:
දී ඇති දත්ත: L1 = 10 mH, L2 = 15 mH සහ M = 10 mH
සේරියානුව පිළිබඳ සූත්රයට අනුව,

එම සමීකරණය භාවිතා කිරීමෙන්, ඔවුන් සේරියානුව පිළිබඳව සම්බන්ධ කළ විට 45 mH යන සමාන ඉන්දක්ත්වය ලබා ගත හැකිය.
උදාහරණය 2
තොරතුරා ප්රකාශනය ඇති දෙක් ධාරා පිළිබඳව 10 mH සහ 15 mH යන ස්ව ඉන්දක්ත්වයන් සහ එක් ධාරා පිළිබඳව 10 mH යන සම්බන්ධ ඉන්දක්ත්වය ඇත. ඔවුන් සේරියානුව නිලින් සම්බන්ධ කළ විට සමාන ඉන්දක්ත්වය සොයන්න.
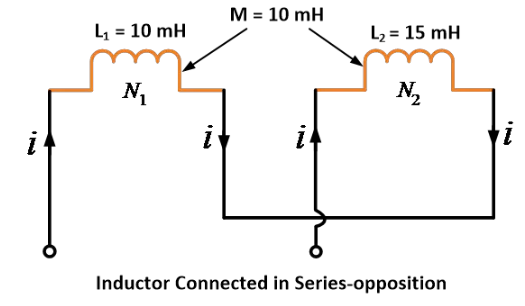
පිළිතුර:
දී ඇති දත්ත: L1 = 10 mH, L2 = 15 mH සහ M = 10 mH
සේරියානුව නිලින් සම්බන්ධ කිරීමේ සූත්රයට අනුව,

එක්සත් කරන ලද ප්රතිඵලය 5 mH වන අතර ඔවුන් බොහෝම ප්රතිවිරුද්ධව සම්බන්ධ කරන විට සමීකරණය භාවිතා කිරීමෙන් එය ලබා ගත හැකිය.
සමාන්තරව සම්බන්ධ කරන ලද ඉන්ඩක්ටරයේ සමීකරණය
සමාන්තරව ඉන්ඩක්ටරයේ එක්සත් කිරීමේ ක්රමය
දෙක් ඉන්ඩක්ටරයේ සමාන්තරව සම්බන්ධ කළ හැකිය
සමාන්තරව උගුල් (කැළැක්කාරී) සම්බන්ධය (පරස්පරව ආර්ථික උත්පාදනය ස්වයම්-ආර්ථික උත්පාදනයන්ට උගුල් වේ)
දෙක් ඉන්ඩක්ටරයේ සමාන්තරව උගුල් කළ විට පරස්පරව ආර්ථික උත්පාදනය ස්වයම්-ආර්ථික උත්පාදනයන්ට උගුල් වේ යැයි පහත දැක්වෙන රූපයේ පෙන්වා ඇත.
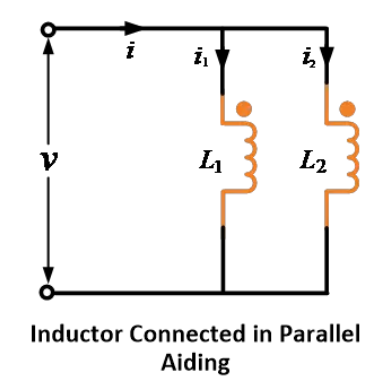
L1 සහ L2 ඉන්ඩක්ටරයේ ට්රාවේස් කරන අතර i1 සහ i2 යනු ටොටල් ට්රාවේස් I නිසා ට්රාවේස් කරන අතර ට්රාවේස් වශයෙන් ටොටල් ට්රාවේස් යැයි ප්රකාශ කරනු ලැබේ.
එබැවින්,
(7) 
ඉන්,
(8) 
මීට අනුව, එක් එක් ප්රතිස්ථාපනයකදී දෙක් EMFs නිශ්චිත කොට ලැබේ. එකක් ස්ව ප්රතිස්ථාපනයේදී පිළිබඳ යන අතර අනෙක්ක් ප්රතිමුහුණු ප්රතිස්ථාපනයේදී පිළිබඳ.
ප්රතිස්ථාපනයන් පරාලියේ සම්බන්ධ කරන ලදී, EMFs සමාන වේ.
ඉන්,
(9) 


(10) 
දැන්, සමීකරණය (9) ට සමීකරණය (8) එකට ආදේශ කිරීමෙන්,

(11) 
මෙහිදී  යනු සම්පාර්ශව සම්බන්ධ කරන ලද පෝලීන්ගේ සමාන පෝලීනයක් නම්, එහිදී ප්රතිඵලයට ලක්වනු ඇති ඉලෙක්ට්රොමොටිව් බලය
යනු සම්පාර්ශව සම්බන්ධ කරන ලද පෝලීන්ගේ සමාන පෝලීනයක් නම්, එහිදී ප්රතිඵලයට ලක්වනු ඇති ඉලෙක්ට්රොමොටිව් බලය
(12) 
මෙය කිසියම් එක් ප්රදේශයක් තුළ ප්රතිඵලයට ලක්වන ඉලෙක්ට්රොමොටිව් බලයට සමාන වේ,

(13) ![Rendered by QuickLaTeX.com \begin{equation*} \frac{di}{dt} = \frac{1}{L_e_q_.} [L_1 \frac{di_1}{dt} + M \frac{di_2}{dt}] \end{equation*}](https://www.electrical4u.com/wp-content/ql-cache/quicklatex.com-7dfa0ff7587394b05eab7bb70894c37b_l3.png?ezimgfmt=rs:199x41/rscb38/ng:webp/ngcb38)
ගැටලුව (10) ට ඇති  අගය (13) ට ආදේශ කරන විට,
අගය (13) ට ආදේශ කරන විට,
![Rendered by QuickLaTeX.com \begin{align*} \frac{di}{dt} = \frac{1}{L_e_q_.} [L_1 (\frac{L_2 - M}{L_1 - M}) \frac{di_2}{dt} + M \frac{di_2}{dt}] \end{align*}](https://www.electrical4u.com/wp-content/ql-cache/quicklatex.com-01480d0a937f35f974ea9daef273f5ed_l3.png?ezimgfmt=rs:277x42/rscb38/ng:webp/ngcb38)
(14) ![Rendered by QuickLaTeX.com \begin{equation*} \frac{di}{dt} = \frac{1}{L_e_q_.} [L_1 (\frac{L_2 - M}{L_1 - M}) + M] \frac{di_2}{dt} \end{equation*}](https://www.electrical4u.com/wp-content/ql-cache/quicklatex.com-8b18bef639f686e78696071ff788946e_l3.png?ezimgfmt=rs:251x41/rscb38/ng:webp/ngcb38)
දැන්, (11) සමීකරණය (14) සමීකරණයට සමාන කරන්න,
![Rendered by QuickLaTeX.com \begin{align*} 1+(\frac{L_2 - M}{L_1 - M}) \frac{di_2}{dt} = \frac{1}{L_e_q_.}[L_1 (\frac{L_2 - M}{L_1 - M}) + M]\frac{di_2}{dt} \end{align*}](https://www.electrical4u.com/wp-content/ql-cache/quicklatex.com-7dcf45ab7172453426ba64e8b1300ae9_l3.png?ezimgfmt=rs:368x42/rscb38/ng:webp/ngcb38)
![Rendered by QuickLaTeX.com \begin{align*} \frac{L_1+L_2 - 2M}{L_1 - M} = \frac{1}{L_e_q_.} [\frac{L_1L_2- L_1M+L_1M - M^2}{L_1 - M}] \end{align*}](https://www.electrical4u.com/wp-content/ql-cache/quicklatex.com-bae7258f22523dff45c6dcd5f18fd8d4_l3.png?ezimgfmt=rs:392x46/rscb38/ng:webp/ngcb38)
![Rendered by QuickLaTeX.com \begin{align*} \frac{L_1+L_2 - 2M}{L_1 - M} = \frac{1}{L_e_q_.} [\frac{L_1L_2 - M^2}{L_1 - M}] \end{align*}](https://www.electrical4u.com/wp-content/ql-cache/quicklatex.com-b0aaa2b67e6a35873ea9217b14f72dba_l3.png?ezimgfmt=rs:272x46/rscb38/ng:webp/ngcb38)
(15) 
පෙළ සමීකරණය දෙකක් පරාලිත කිරීම හෝ එකතුවූ සම්බන්ධතාවක් ඇති නිසා ප්රතිඵලය ලබා දෙයි.
දෙක් පැහැයේ අතර තුළුම් බාධාවක් නැති නම් (එනම්, M = 0),

සමාන්තර එකිනෙකට ප්රතිවිරුද්ධ (විශේෂ සම්බන්ධය) සම්බන්ධය (පරස්පරව උත්පාදනය කරන විද්යුත් ධාවය ස්වයං උත්පාදනය කරන EMF ලෙස ප්රතිවිරුද්ධයක්)
දෙකම ඉන්ඩක්ටර් සමාන්තරව එකිනෙකට ප්රතිවිරුද්ධව සම්බන්ධ කළ විට, පරස්පරව උත්පාදනය කරන විද්යුත් ධාවය ස්වයං උත්පාදනය කරන EMF ලෙස ප්රතිවිරුද්ධයක් වේ.
හෝඩාගැනීමට පහත රූපයේ දැක්වෙන්නේ දෙකම ඉන්ඩක්ටර් සමාන්තරව එකිනෙකට ප්රතිවිරුද්ධව හෝ විශේෂ සම්බන්ධයකි.
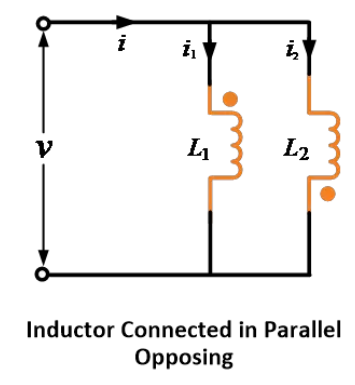
සමාන්තර ආදාන සම්බන්ධය වැනි ආකාරයකින්, මෙය පෙන්විය හැකිය,
(16) 
ඉහත සමීකරණය දෙකම ඉන්ඩක්ටර් සමාන්තරව එකිනෙකට ප්රතිවිරුද්ධව හෝ විශේෂ සම්බන්ධයකින් සම්බන්ධ කරන්නේ සමාන්තර එකිනෙකට ප්රතිවිරුද්ධ සමාන්තර ඉන්ඩක්ටැන්ස් ලෙස පෙන්විය හැකිය.
දෙකම කොල් අතර පරස්පර ඉන්ඩක්ටැන්ස් නැති අතර (එනම්, M = 0), නම්,

නිදසුන 1
මීටර 5 වල සහ මීටර 10 වල ස්වයං ප්රතික්රියාකාරීත්වයක් සහිත දෙක් ඉන්ඩක්ටරයන් ඇත. එවැනි ඉන්ඩක්ටරයන් දෙක අතර ප්රතික්රියාකාරීත්වය මීටර 5 වේ. ඇනුව නිර්මාණය කිරීමට ප්රතිඵල ප්රතික්රියාකාරීත්වය සොයන්න.
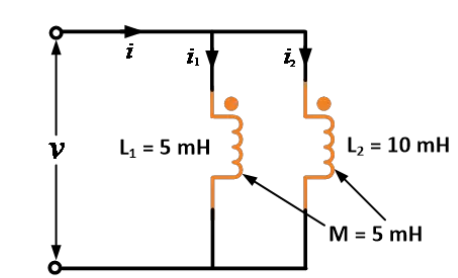
පිළිතුර:
දී ඇති තොරතුරු: L1 = 5 mH, L2 = 10 mH සහ M = 5 mH
සමාන්තර ප්රතිඵල සූත්රය අනුව,

ඉන්ඩක්ටරයන් දෙක සමාන්තරව නිර්මාණය කිරීමට ප්රතිඵල ප්රතික්රියාකාරීත්වය 5 mH වේ.
නිදසුන 2
දෙක් ප්රතිඵලකයන්ගේ ස්ව-ප්රතිඵලකතාව 5 mH සහ 10 mH වන අතර එක් ප්රතිඵලකයක් අනෙකුත් ප්රතිඵලකයට ඇති ප්රතිඵලකතාව 5 mH වේ. මෙම ප්රතිඵලකයන් පරිපූර්ණ ලෙස ප්රතිකුල කිරීමෙන් සම්බන්ධ කළ විට සම්බන්ධ ප්රතිඵලකතාව සොයන්න.
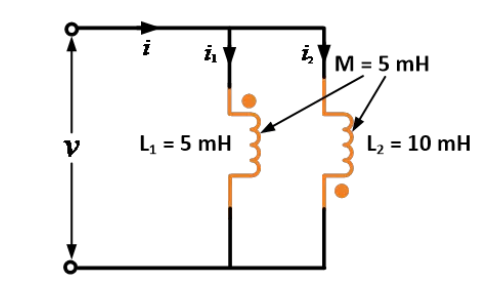
පිළිතුර:
දී ඇති දත්ත: L1 = 5 mH, L2 = 10 mH සහ M = 5 mH
පරිපූර්ණ ලෙස ප්රතිකුල කිරීමේ සූත්රය අනුව,

එබැවින්, සූත්රය භාවිතා කිරීමෙන්, පරිපූර්ණ ලෙස ප්රතිකුල කිරීමෙන් සම්බන්ධ කළ විට සම්බන්ධ ප්රතිඵලකතාව 1 mH වේ.
යුගල ප්රතිඵලකයන්
එක් ප්රතිඵලකයේ උත්තර ප්රදේශය තවත් ප්රතිඵලකයේ පිටුපස් ප්රදේශය හෝ ආරුකිරීම් වලට ප්රතිඵලක වන විට, එම ප්රතිඵලක යුගලය ප්රතිඵලක යුගලයක් ලෙස හැඳින්වේ. යුගල ප්රතිඵලක යුගලයන් අතර ප්රතිඵලක ප්රතිඵලකතාව සිටිය හැකිය.
යුගල ප්රතිඵලක ප්රදේශයන් තුළ, එක් ප්රතිඵලකයක් ප්රදේශය යොදා ගැනීමෙන් එක් ප්රතිඵලකයේ බලය තවත් ප්රතිඵලකයට යොමු වේ. දෙක් ප්රතිඵලක ට්රාන්ස්ෆොර්මරය, ඉතිරිකරණ ට්රාන්ස්ෆොර්මරය, සහ ඉතිරිකරණ මොටරය යුගල ප්රතිඵලක ප්රදේශයන්, ප්රතිඵලක ප්රදේශයන්, හෝ ප්රතිඵලක ප්රදේශයන් සඳහා උදාහරණ වේ.
මූලද්රව්ය බල සම්බන්ධ ඉඩියන් යනු හෝ කොයිල් යනු 1 සහ 2 දෙකටම L1 සහ L2 ලෙස ඉඩියන් ඇති බව සැලකිය යුතුය. මෙම කොයිල් දෙක අතර ප්රතිපාදන ඉඩියනය M ලෙස සලකනු ලැබේ.
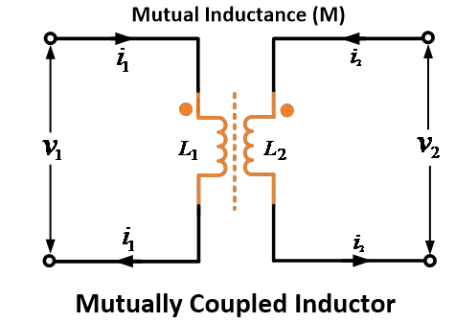
ප්රතිපාදන ඉඩියනයේ නියැළිය යනු (L1 + M සහ L2 + M) හෝ අඩු කිරීමයි (L1 – M සහ L2 – M) යන දෙකෙන් එකක් විය හැකිය. මෙය කොයිල් දෙකේ පිළිබඳ උපක්රමණය මත පදනම් වේ.
කොයිල් දෙක පිළිබඳ උපක්රමණය අනුව ඔවුන්ගේ තුන්පැත්තන් පිළිගැනීමට පිළිබඳ නම්, එක් කොයිල් එකක ඉඩියනය L1 + M සඳහා කොයිල් 1 සහ L2 + M සඳහා කොයිල් 2 ලෙස දිගු කරනු ලැබේ. එය නිසාම එක් කොයිල් එකක පිළිගැනීමට පිළිබඳ ප්රමාණය එහි එක් එක් ප්රමාණයට පිළිතුරු ප්රමාණයට අඩු වේ.
කොයිල් දෙක පිළිබඳ උපක්රමණය අනුව ඔවුන්ගේ තුන්පැත්තන් ආරෝපණය කිරීමට පිළිබඳ නම්, එක් කොයිල් එකක ඉඩියනය L1 – M සඳහා කොයිල් 1 සහ L2 – M සඳහා කොයිල් 2 ලෙස අඩු කරනු ලැබේ. එය නිසාම එක් කොයිල් එකක පිළිගැනීමට පිළිබඳ ප්රමාණය එහි එක් එක් ප්රමාණයට පිළිතුරු ප්රමාණයට අඩු වේ.
ප්රතිපාදන ඉඩියන සූත්රය
අපි දන්නා පරිදි, එක් කොයිල් එකක පරිදි ධාරාවේ කෝණයක් විශේෂයක් මෙන්ම දෙවැනි කොයිල් එකක ප්රතිපාදන රෝත් ප්රතිපාදනය මෙන්ම දිගු කිරීම මගින් පිළිවෙලින් සිදු කරනු ලැබේ.
ප්රතිපාදන ඉඩියනය යනු එක් කොයිල් (හෝ ප්රවාහය) එකක් දෙවැනි කොයිල් (හෝ ප්රවාහය) එකකට ප්රතිපාදන රෝත් ප්රතිපාදනය මෙන්ම දිගු කිරීමට එක් කොයිල් එකක ධාරාවේ කෝණයක් විශේෂයක් මෙන්ම වෙනස් කිරීමට නියැළිය වන පිළිබඳ නියැළියකි.
වෙනත් පිළිවෙලකින්, දෙක් කොයිල් දෙකේ බිම ප්රතිපාදන ඉඩියනය යනු, එක් කොයිල් එකක ධාරාවේ කෝණයක් විශේෂයක් වෙනස් කිරීමට පිළිබඳ ප්රතිරෝධය වන බිමකි. මෙය ප්රතිපාදනය නිසාම දෙවැනි කොයිල් එකක ප්රතිපාදන රෝත් ප්රතිපාදනය මෙන්ම දිගු කිරීමට එක් කොයිල් එකක ධාරාවේ කෝණයක් වෙනස් කිරීමට පිළිබඳ ප්රතිරෝධය ඇති බැවිනි.
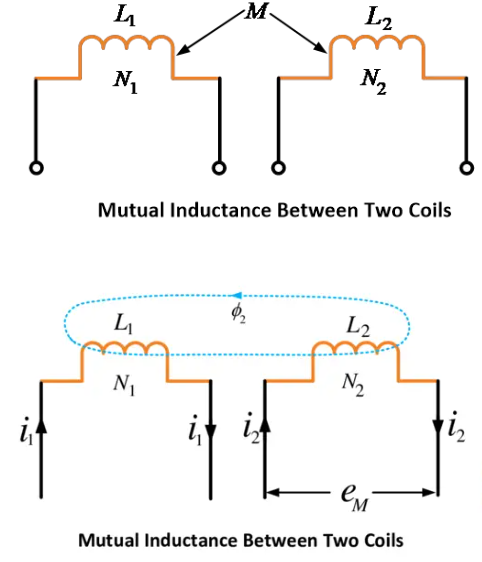
ප්රතිපාදන ඉඩියනය (M) යනු එක් කොයිල් එකක ප්රතිපාදන රෝත් ප්රතිපාදනය මෙන්ම දිගු කිරීමට පිළිබඳ නියැළියකි, එනම් එක් කොයිල් එකක ප්රතිපාදන රෝත් ප්රතිපාදනය මෙන්ම දිගු කිරීමට පිළිබඳ නියැළියකි.
ගණිතමයව,

කොටස්,
 = පළමු කෝයිල් උපරිම ධාරාව
= පළමු කෝයිල් උපරිම ධාරාව
 = දෙවන කෝයිල් ට සම්බන්ධ වන හීන්දුව
= දෙවන කෝයිල් ට සම්බන්ධ වන හීන්දුව
 = දෙවන කෝයිල් ට සම්බන්ධ වන රැස්සුවේ ගණන
= දෙවන කෝයිල් ට සම්බන්ධ වන රැස්සුවේ ගණන
දෙක් කෝයිල්වල අතර සම්බන්ධ නූතනත්වය 1 හෙන්රි ලෙස අර්ථ දක්වනු ලැබේ එක් කෝයිල් ට 1 ඇම්පීර් ප්රති සැක්කේ ප්රවේගයක් වෙනස් වන ප්රකාශයේදී අනෙක් කෝයිල් ට 1 V යාන්ත්රික තාවකයක් ආරෝපිත කරන ලදී.
සම්බන්ධ මානය
දෙක් කෝයිල්වල අතර සම්බන්ධ මානය (k) යනු එක් කෝයිල් ට ප්රති දිගේ වැදුණු ධාරාව ඉදිකිරීමේදී ඇතිවන මාග්නෙටික හීන්දුව ප්රමාණය සම්බන්ධ කරන ප්රමාණයයි.
කෝප්ලින් පාරමිතිය යනු කෝප්ලි පරිගණක විද්යුත් ප්රබේධ ප්රතික්රියාවට අත් සම්බන්ධ කොළ අතර ඇති ආසන්නතාවය ටීමින් සැලකෙන ලද විශේෂ පාරමිතියකි.
ගණිතමය ලෙස, කෝප්ලින් පාරමිතිය පහත පරිදි දර්ශක කළ හැකිය,

උදාහරණයක් ලෙස,
L1 යනු පළමු කොළයේ එක් නියුත් ප්රතික්රියාවයි
L2 යනු දෙවන කොළයේ එක් නියුත් ප්රතික්රියාවයි
M යනු දෙක් කොළ අතර ප්රායෝගික නියුත් ප්රතික්රියාවයි
කෝප්ලින් පාරමිතිය දෙක් කොළ අතර ප්රායෝගික නියුත් ප්රතික්රියාවෙන් බැලූ ප්රතිඵලයකි. කෝප්ලින් පාරමිතිය වැඩි වීමෙන් ප්රායෝගික නියුත් ප්රතික්රියාවද වැඩි වේ. දෙක් කොළ මාග්නෑටික ත්රාස් මගින් ප්රායෝගික කර ඇත.
එක් කොළයේ පුරා ත්රාස් අනෙක් කොළයට යොමු වූ විට, කෝප්ලින් පාරමිතිය 1 (ඉන්නේ 100%) නම්, කොළ අතර ප්රචණ්ඩ ආසන්නතාවයක් ඇති බව කියනු ලැබේ.
එක් කොළයේ චාරිකාවේ අරා පුද්ගලයා අනෙක් කොළයට යොමු වූ විට, කෝප්ලින් පාරමිතිය 0.5 (ඉන්නේ 50%) නම්, කොළ අතර විශාල ආසන්නතාවයක් ඇති බව කියනු ලැබේ.
එක් කොළයේ ත්රාස් අනෙක් කොළයට යොමු නොවූ විට, කෝප්ලින් පාරමිතිය 0, කොළ අතර ප්රමාණයෙන් වෙන් කොට ඇති බව කියනු ලැබේ.
කෝප්ලින් පාරමිතිය සැලකිය යුතුයි ප්රමාණයෙන් අඩු විය යුතුය. එය භාවිතා කරන රේඛා විශේෂයන් මත පදනම් වේ. අන්තර් පාරමිතියක් සඳහා, කෝප්ලින් පාරමිතිය 0.4 සිට 0.8 දක්වා විය හැකිය කොළ දෙක අතර අවකාශය මත පදනම් වේ, එහිදී අයිරන් හෝ ෆෙරයිට් පාරමිතියක් සඳහා එය 0.99 දක්වා විය හැකිය.
ආදාන: Electrical4u.
කියවීම: මුල් පියවරට ආදරණිය, ජාවිත් ලිපි බෙදා ගැනීමට අවශ්ය, කාර්යක්ෂමතාවක් ඇති නම් අවියා ගැනීමට අවශ්යයි.






































