インダクタとは何か
インダクタ(または電気インダクタ)は、二端子のパッシブ電気要素であり、電流が流れると磁場の形でエネルギーを貯蔵します。また、コイル、チョーク、またはリアクターとも呼ばれます。
インダクタは単純に導線のコイルです。通常は絶縁された銅のような導体材料をプラスチックや強磁性体の中に入れて巻いたもので、これを鉄心インダクタと呼びます。
インダクタは通常、1 µH(10-6 H)から20 Hの範囲で利用可能です。多くのインダクタには、コイル内にフェライトや鉄で作られた磁心があり、これにより磁場が増大し、その結果インダクタンスも増大します。
ファラデーの電磁誘導の法則によれば、インダクタまたはコイルを通る電流が変化すると、時間的に変化する磁場によってe.m.f(起電力)または電圧が生じます。インダクタに発生する誘導電圧または起電力は、インダクタを通る電流の変化率に比例します。
インダクタンス(L)は、コイルに流れる電流の大きさや方向の変化に抵抗するコイルの特性です。コイルのインダクタンスが大きいほど、磁場の形で電気エネルギーを蓄積する能力も大きくなります。
コイルはどのように機能するのか?
回路内のコイルは、その中に流れる電流の変化に対し、その変化率に比例する電圧を誘起することで抵抗します。コイルが回路内でどのように機能するか理解するためには、以下の画像をご覧ください。
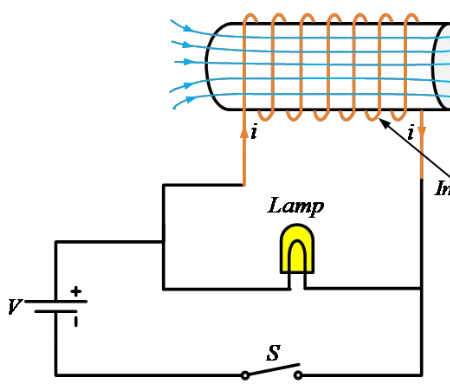 回路内のコイルの動作
回路内のコイルの動作
図のように、ランプ、ワイヤーのコイル(コイル)、およびスイッチがバッテリーに接続されています。コイルを取り除いた場合、ランプは通常通り点灯します。しかし、コイルがあると、回路の挙動は完全に異なります。
コイルまたはコイルの抵抗はランプよりもずっと低いので、スイッチを閉じると、コイルを通る電流がほとんど流れ始めます。そのため、ランプは非常に暗く光ることが期待されます。
しかし、コイルの回路内での挙動により、スイッチを閉じるとランプは明るく光り、徐々に暗くなり、スイッチを開けるとランプは非常に明るく光り、すぐに消えます。
これは、コイルに電圧または電位差が加えられると、コイルを通る電流によって磁界が生じ、この磁界がコイルに逆極性の誘導電流を生じさせるからです。レンツの法則によれば、これが起こります。
この誘導電流は、コイルの磁界によって生じ、電流の増加または減少といった変化を抵抗します。磁界が形成されると、電流は正常に流れることができます。
スイッチを閉じたとき、コイル周辺の磁界はコイル内の電流を維持し続け、磁界が崩壊するまで電流が流れ続けます。これにより、スイッチが開いていても一定時間ランプが光り続けます。
つまり、コイルは磁界の形でエネルギーを蓄積し、通過する電流の変化に抵抗しようとします。したがって、コイルを通る電流は瞬時に変化することはできません。
コイルの回路記号
コイルの回路記号は以下の画像に示されています。
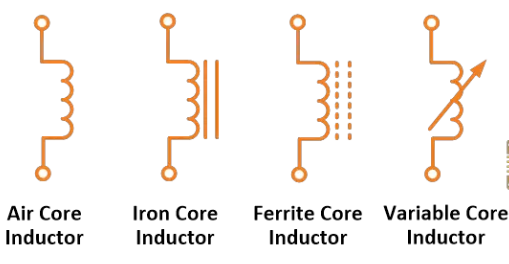
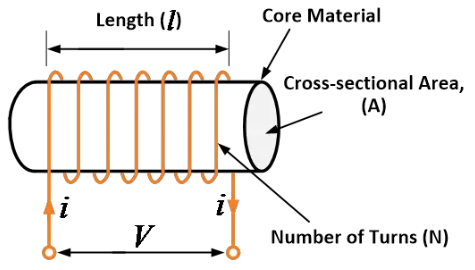 インダクターシンボル
インダクターシンボル
インダクター方程式
インダクターの電圧
インダクターにかかる電圧は、インダクターを流れる電流の変化率に比例します。数学的には、インダクターにかかる電圧は以下の式で表されます。

ここで、 = インダクターにかかる瞬時電圧(V)、
= インダクターにかかる瞬時電圧(V)、
 = インダクタンス(H)、
= インダクタンス(H)、
 = 電流の変化率(A/s)
= 電流の変化率(A/s)
インダクタの電圧は、インダクタの磁界に蓄えられたエネルギーによるものです。
もし直流がインダクタを通過する場合、 は時間に対して一定であるため、ゼロになります。したがって、インダクタの電圧もゼロになります。つまり、直流の場合、定常状態ではインダクタはショート回路として機能します。
は時間に対して一定であるため、ゼロになります。したがって、インダクタの電圧もゼロになります。つまり、直流の場合、定常状態ではインダクタはショート回路として機能します。
インダクタを通る電流
インダクタを通る電流は、その両端に発生する電圧を使って次のように表すことができます。

上記の方程式では、積分の範囲は過去の履歴または初期条件に基づいて決定されます。つまり、 からです。
からです。
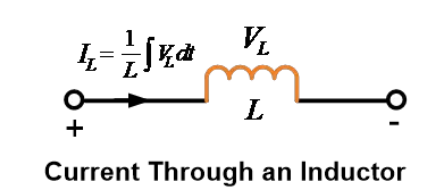
ここで、スイッチング動作がt=0で行われると仮定すると、つまりスイッチがt=0で閉じられると、インダクタを通る電流の方程式は次のようになります。

積分範囲を2つの区間に分割することができます。 と
と  です。私たちは、
です。私たちは、 はスイッチング動作が行われる直前の瞬間であり、
はスイッチング動作が行われる直前の瞬間であり、 はスイッチング動作が行われた直後の瞬間であることを知っています。したがって、以下のように書くことができます。
はスイッチング動作が行われた直後の瞬間であることを知っています。したがって、以下のように書くことができます。

したがって、

ここで、項  は、インダクタ電流の過去の値を示しており、これは
は、インダクタ電流の過去の値を示しており、これは  の初期条件に他なりません。これを
の初期条件に他なりません。これを  と表記します。
と表記します。

時刻  において、以下のようになります。
において、以下のようになります。

当初、スイッチング動作がゼロ時間で行われると仮定しました。そのため、 から
から までの積分はゼロです。
までの積分はゼロです。
したがって、

したがって、インダクタを通る電流は瞬時に変化することはできません。つまり、スイッチング動作の前後でインダクタを通る電流は同じです。
t=0でのインダクタ
インダクタの つまり、インダクタに電圧を切り替える瞬間の電圧は理想的には
つまり、インダクタに電圧を切り替える瞬間の電圧は理想的には であり、時間間隔
であり、時間間隔 がゼロであるため、スイッチング時にインダクタは開放回路として作用します。一方、定常状態では
がゼロであるため、スイッチング時にインダクタは開放回路として作用します。一方、定常状態では においてショート回路として作用します。
においてショート回路として作用します。
スイッチング動作前にインダクタが初期電流I0を持つ場合、瞬間 において、その値は
において、その値は の一定電流源として作用し、定常状態では
の一定電流源として作用し、定常状態では において、電流源の両端でショート回路として作用します。
において、電流源の両端でショート回路として作用します。
直列および並列インダクタ
直列および並列のインダクタは、直列および並列の抵抗器と同様に動作します。磁気的に結合しているコイル1とコイル2を考えます。自己インダクタンス  と
と  があります。Mをヘンリー単位の二つのコイル間の相互インダクタンスとします。
があります。Mをヘンリー単位の二つのコイル間の相互インダクタンスとします。
電気回路内の二つのインダクタは、異なる方法で接続され、それによって等価インダクタンスの値が異なります。
直列インダクタの公式
直列インダクタの追加方法
二つの互いに結合したインダクタまたはコイルが直列に接続されている回路を考えます。インダクタを直列に接続する方法は二つあります。
インダクタ1の自己インダクタンスを とし、インダクタ2の自己インダクタンスを
とし、インダクタ2の自己インダクタンスを とする。両インダクタは相互インダクタンス Mで結合されている。
とする。両インダクタは相互インダクタンス Mで結合されている。
直列補助(累積)接続(相互に誘導された電動力が自己誘導された電動力を補助する)
以下の画像に示すように、2つのインダクタまたはコイルは直列補助または累積的に接続される。
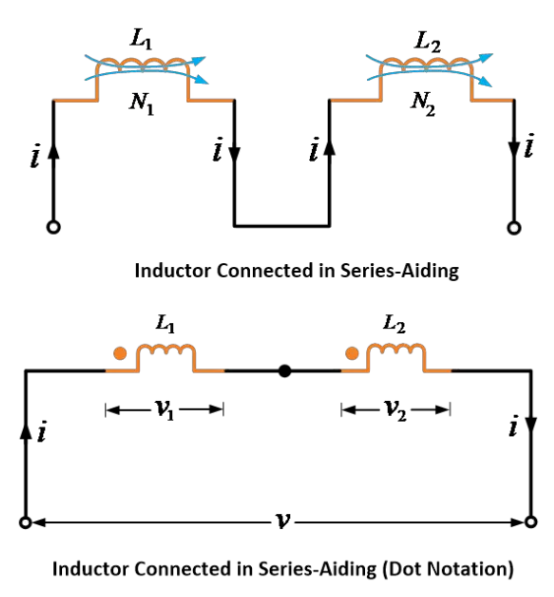
この接続では、両インダクタの自己および相互磁束が同じ方向に作用するため、自己および相互に誘導された電動力も同じ方向となる。
したがって、
インダクタ1の自己誘導電動力、
インダクタ1の相互誘導電動力、
インダクタ2の自己誘導電動力、
インダクタ1の相互誘導起電力,
組み合わせでの総誘導起電力,

(1) 
もし が直列補助接続の2つのインダクタの等価インダクタンスである場合、組み合わせでの誘導起電力は以下の式で与えられる。
が直列補助接続の2つのインダクタの等価インダクタンスである場合、組み合わせでの誘導起電力は以下の式で与えられる。
(2) 
式(1)と式(2)を比較すると、
(3) 
上記の式は、累積または加算的に接続された2つの直列インダクタまたはコイルの等価インダクタンスを示しています。
2つのコイル間に相互インダクタンスがない場合(つまり、M = 0の場合)、

直列反対接続(差動接続)(相互誘導電圧が自己誘導電圧に反対する)
以下の画像に示すように、2つの相互結合したインダクタまたはコイルが直列に接続され、それぞれのインダクタによって生じる磁束が互いに反対方向となる回路を考えます。
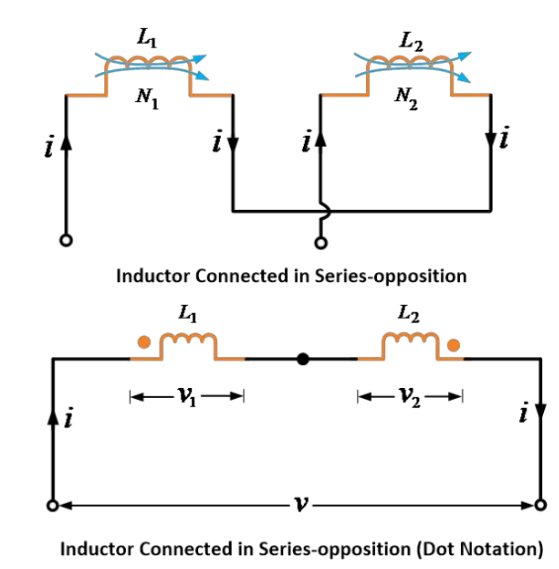
磁束が反対方向であるため、相互誘導電圧の符号は自己誘導電圧の符号と逆になります。したがって、
インダクタ1の自己誘導電圧,
インダクタ1の相互誘導起電力,
インダクタ2の自己誘導起電力,
インダクタ2の相互誘導起電力,
組み合わせでの総誘導起電力は、

(4) 
もし が直列反対接続の2つのインダクタの等価インダクタンスであれば、組み合わせでの誘導起電力は以下の式で与えられる。
が直列反対接続の2つのインダクタの等価インダクタンスであれば、組み合わせでの誘導起電力は以下の式で与えられる。
(5) 
式(4)と式(5)を比較すると、
(6) 
上記の式は、2つのコイルが直列反対接続または差動接続された場合の等価インダクタンスを示しています。
2つのコイル間に相互インダクタンスがない場合(つまり、M = 0の場合)、

例1
2つのコイルの自己インダクタンスがそれぞれ10 mHと15 mHで、2つのコイル間の相互インダクタンスが10 mHである場合、それらが直列助長接続されたときの等価インダクタンスを求めなさい。
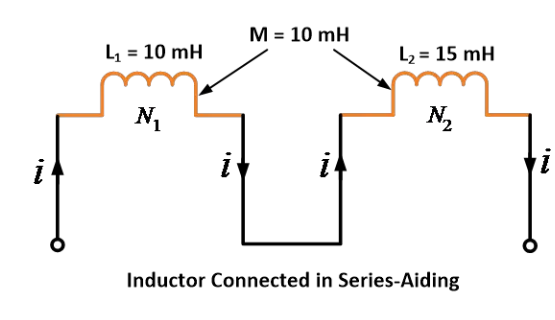
解決策:
与えられたデータ: L1 = 10 mH, L2 = 15 mH および M = 10 mH
直列補助公式によると、

したがって、この式を使用して、それらが直列補助で接続されたときの等価インダクタンスは45 mHであることがわかります。
例2
2つのコイルの自己インダクタンスはそれぞれ10 mHと15 mHであり、2つのコイル間の相互インダクタンスは10 mHです。それらが直列反対に接続されたときの等価インダクタンスを求めなさい。
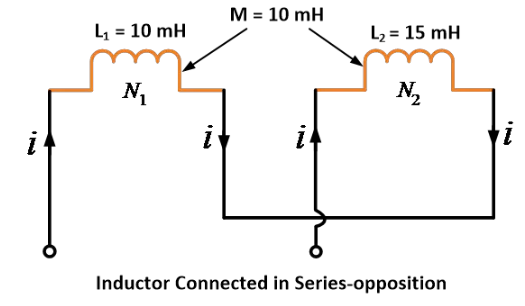
解決策:
与えられたデータ: L1 = 10 mH, L2 = 15 mH および M = 10 mH
直列反対公式によると、

したがって、この式を使用して、それらが直列反対接続されている場合の等価インダクタンスは5 mHであることがわかります。
並列インダクタの公式
インダクタを並列に接続する方法
2つのインダクタは以下のようになるように並列に接続することができます
並列補助接続(相互誘導起電力が自己誘導起電力を補助する)
2つのインダクタが並列補助接続されている場合、相互誘導起電力は自己誘導起電力を補助します。下図をご覧ください。
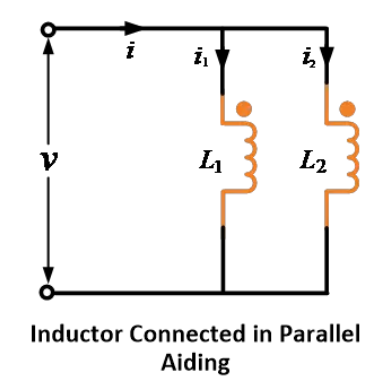
L1とL2を通る電流をそれぞれi1およびi2とし、合計電流をIとします。
したがって、
(7) 
したがって、
(8) 
各コイルには、自己誘導と相互誘導による2つの電動力が発生します。
コイルが並列に接続されているため、電動力は等しくなります。
したがって、
(9) 


(10) 
次に、式(9)を式(8)に入れると以下のようになります。

(11) 
もし が並列接続されたインダクタの等価インダクタンスである場合、それによって誘起される電動力は次のようになります。
が並列接続されたインダクタの等価インダクタンスである場合、それによって誘起される電動力は次のようになります。
(12) 
これは任意のコイルに誘起される電動力と等しいです。つまり、

(13) ![Rendered by QuickLaTeX.com \begin{equation*} \frac{di}{dt} = \frac{1}{L_e_q_.} [L_1 \frac{di_1}{dt} + M \frac{di_2}{dt}] \end{equation*}](https://www.electrical4u.com/wp-content/ql-cache/quicklatex.com-7dfa0ff7587394b05eab7bb70894c37b_l3.png?ezimgfmt=rs:199x41/rscb38/ng:webp/ngcb38)
方程式 (10) の  の値を方程式 (13) に代入すると
の値を方程式 (13) に代入すると
![Rendered by QuickLaTeX.com \begin{align*} \frac{di}{dt} = \frac{1}{L_e_q_.} [L_1 (\frac{L_2 - M}{L_1 - M}) \frac{di_2}{dt} + M \frac{di_2}{dt}] \end{align*}](https://www.electrical4u.com/wp-content/ql-cache/quicklatex.com-01480d0a937f35f974ea9daef273f5ed_l3.png?ezimgfmt=rs:277x42/rscb38/ng:webp/ngcb38)
(14) ![Rendered by QuickLaTeX.com \begin{equation*} \frac{di}{dt} = \frac{1}{L_e_q_.} [L_1 (\frac{L_2 - M}{L_1 - M}) + M] \frac{di_2}{dt} \end{equation*}](https://www.electrical4u.com/wp-content/ql-cache/quicklatex.com-8b18bef639f686e78696071ff788946e_l3.png?ezimgfmt=rs:251x41/rscb38/ng:webp/ngcb38)
次に、方程式 (11) を方程式 (14) と等しくします。
![Rendered by QuickLaTeX.com \begin{align*} 1+(\frac{L_2 - M}{L_1 - M}) \frac{di_2}{dt} = \frac{1}{L_e_q_.}[L_1 (\frac{L_2 - M}{L_1 - M}) + M]\frac{di_2}{dt} \end{align*}](https://www.electrical4u.com/wp-content/ql-cache/quicklatex.com-7dcf45ab7172453426ba64e8b1300ae9_l3.png?ezimgfmt=rs:368x42/rscb38/ng:webp/ngcb38)
![Rendered by QuickLaTeX.com \begin{align*} \frac{L_1+L_2 - 2M}{L_1 - M} = \frac{1}{L_e_q_.} [\frac{L_1L_2- L_1M+L_1M - M^2}{L_1 - M}] \end{align*}](https://www.electrical4u.com/wp-content/ql-cache/quicklatex.com-bae7258f22523dff45c6dcd5f18fd8d4_l3.png?ezimgfmt=rs:392x46/rscb38/ng:webp/ngcb38)
![Rendered by QuickLaTeX.com \begin{align*} \frac{L_1+L_2 - 2M}{L_1 - M} = \frac{1}{L_e_q_.} [\frac{L_1L_2 - M^2}{L_1 - M}] \end{align*}](https://www.electrical4u.com/wp-content/ql-cache/quicklatex.com-b0aaa2b67e6a35873ea9217b14f72dba_l3.png?ezimgfmt=rs:272x46/rscb38/ng:webp/ngcb38)
(15) 
上記の式は、並列補助または累積接続された2つのインダクタの等価インダクタンスを示しています。
もし2つのコイル間に相互インダクタンスがなければ(つまり、M = 0の場合)、

並列反対接続(差動接続)(相互誘導電圧が自己誘導電圧に反対する)
2つのインダクタが並列反対接続されている場合、相互誘導電圧は自己誘導電圧に反対します。
以下の画像に示すように、2つのインダクタは並列反対または差動で接続されています。
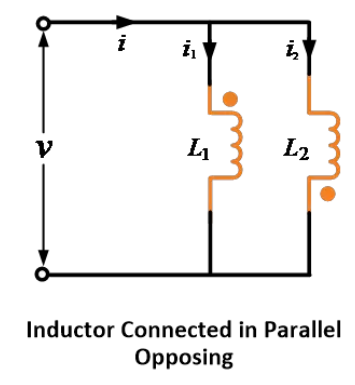
並列補助接続と同様の方法で、以下の式が証明されます。
(16) 
上記の式は、2つのインダクタが並列反対または差動接続されている場合の等価インダクタンスを示しています。
2つのコイル間に相互インダクタンスがない場合(つまり、M = 0の場合)、

例1
自己インダクタンスがそれぞれ5mHと10mH、相互インダクタンスが5mHの2つのインダクタがあります。これらのインダクタが並列助長接続されたときの等価インダクタンスを求めなさい。
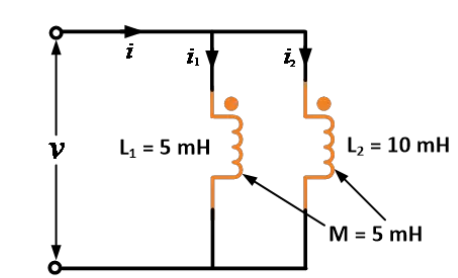
解:
与えられたデータ:L1 = 5 mH, L2 = 10 mH, M = 5 mH
並列助長接続の公式によると、

したがって、この式を使用して、並列助長接続されたときの等価インダクタンスは5mHであることがわかります。
例2
2つのインダクタの自己インダクタンスはそれぞれ5 mHと10 mHで、相互インダクタンスは5 mHです。これらが反対方向に並列接続されたときの等価インダクタンスを求めなさい。
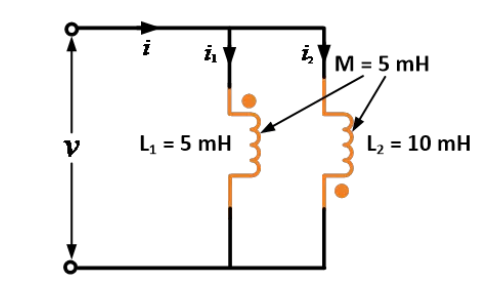
解法:
与えられたデータ: L1 = 5 mH, L2 = 10 mH, M = 5 mH
並列反対向きの公式によれば

したがって、この式を使用して、それらが並列反対向きに接続されたときの等価インダクタンスは1 mHであることがわかります。
結合インダクタ
あるインダクタ(コイル)の磁界が別の隣接するインダクタの巻線を切ったりリンクしたりすると、これらの2つのインダクタは磁気的に結合していると言います。結合インダクタまたはコイルにより、2つのコイル間に相互インダクタンスが存在します。
結合回路では、いずれかの回路が励起されると、エネルギーが一方の回路から他方の回路へ移動します。2巻き変圧器、オートトランスフォーマー、誘導電動機は、磁気的に結合したインダクタまたはコイルまたは回路の例です。
インダクタンス L1 と L2 を持つ磁気結合された2つのコイル1と2を考えます。これらのコイル間の相互インダクタンスを M とします。
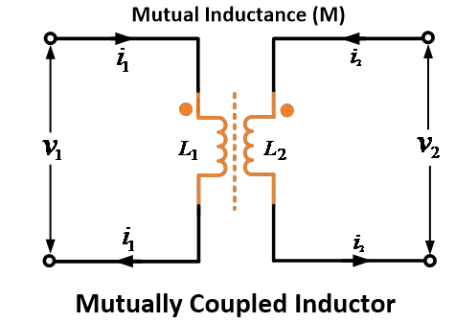
相互インダクタンスの効果は、コイルの配置によって、各コイルのインダクタンスを増加させる(L1 + M および L2 + M)か、または減少させる(L1 – M および L2 – M)かになります。
2つのコイルが互いに磁束を補強するように配置されている場合、各コイルのインダクタンスは M だけ増加し、コイル1では L1 + M となり、コイル2では L2 + M となります。これは、各コイルにリンクする総磁束がそのコイル自身の磁束よりも大きいためです。
2つのコイルが互いに磁束を反対方向にするように配置されている場合、各コイルのインダクタンスは M だけ減少し、コイル1では L1 – M となり、コイル2では L2 – M となります。これは、各コイルにリンクする総磁束がそのコイル自身の磁束よりも小さいためです。
相互インダクタンスの公式
一方のコイルで電流が変化すると、必ず他方のコイルに相互誘導電動力が生じることが知られています。
相互インダクタンスとは、あるコイル(または回路)の電流が変化したときに、近傍の別のコイル(または回路)に誘導により電動力を生じさせる能力を指します。
言い換えると、2つのコイルのそれぞれが、他のコイルの電流の変化を妨げる性質を相互インダクタンスと呼びます。この妨害は、一方のコイルの電流が変化することで、他方のコイルに相互誘導電動力が生じ、これが最初のコイルの電流の変化を妨げることによるものです。
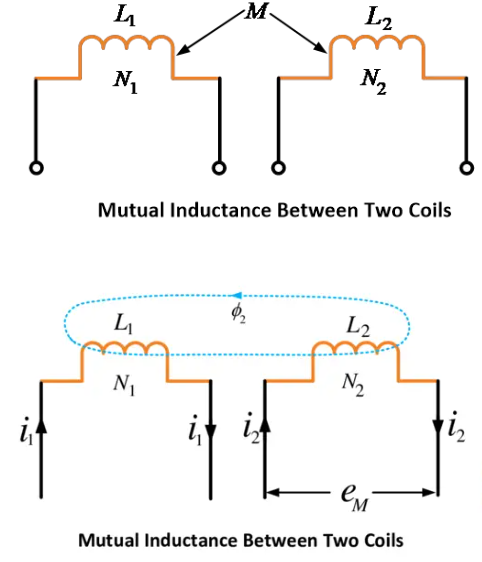
相互インダクタンス(M)は、あるコイルの単位電流に対する他のコイルの磁束連鎖数として定義されます。
数式で表すと

ここで
 = 第一コイルの電流
= 第一コイルの電流
 = 第二コイルにリンクする磁束
= 第二コイルにリンクする磁束
 = 第二コイルの巻数
= 第二コイルの巻数
2つのコイル間の相互インダクタンスは、一方のコイルで1秒あたり1アンペアの速度で変化する電流が他方のコイルに1Vの起電力を誘導する場合、1ヘンリーです。
結合係数
2つのコイル間の結合係数(k)は、一方のコイルの電流によって生じる磁束のうち、他方のコイルにリンクする磁束の割合として定義されます。磁束を参照してください。
結合係数は、誘導結合されたコイル間の結合量を決定するための重要なパラメータです。
数学的には、結合係数は以下の式で表されます。

ここで、
L1 は最初のコイルの自己インダクタンス
L2 は2番目のコイルの自己インダクタンス
M は2つのコイル間の相互インダクタンス
結合係数は2つのコイル間の相互インダクタンスに依存しています。結合係数が高いほど、相互インダクタンスも高くなります。2つの誘導結合されたコイルは磁束によって連結されています。
一方のコイルの全磁束が他方のコイルと連携する場合、結合係数は1(つまり100%)であり、このようなコイルは緊密に結合していると言います。
一方のコイルで生成された磁束の半分だけが他方のコイルと連携する場合、結合係数は0.5(つまり50%)であり、このようなコイルは緩く結合していると言います。
一方のコイルの磁束が全く他方のコイルと連携しない場合、結合係数は0であり、このようなコイルは磁気的に孤立していると言います。
結合係数は常に1未満になります。これは使用されるコア材料によります。エアーコアの場合、結合係数は2つのコイル間の距離に応じて0.4から0.8の範囲となりますが、鉄またはフェライトコアを使用すると0.99まで高くなることがあります。
出典: Electrical4u.
声明: 元の内容を尊重し、良い記事は共有する価値があります。著作権侵害がある場合は削除をお願いします。






































