ਸੀਰੀਜ਼ ਅਤੇ ਸਮਾਂਤਰ ਇੰਡੱਕਟਰ (ਫਾਰਮੂਲਾ ਅਤੇ ਉਦਾਹਰਣ ਸਮੱਸਿਆਵਾਂ)

ਫੀਲਡ: ਬੁਨਿਆਦੀ ਬਿਜਲੀ

China

ਇੰਡਕਟਰ ਕੀ ਹੈ?

ਇੰਡਕਟਰ (ਜਿਸਨੂੰ ਵੀ ਇਲੈਕਟ੍ਰੀਕਲ ਇੰਡਕਟਰ ਕਿਹਾ ਜਾਂਦਾ ਹੈ) ਨੂੰ ਇੱਕ ਦੋ-ਟਰਮਿਨਲ ਪਾਸਿਵ ਇਲੈਕਟ੍ਰੀਕਲ ਤੱਤ ਦੇ ਰੂਪ ਵਿੱਚ ਪਰਿਭਾਸ਼ਿਤ ਕੀਤਾ ਜਾਂਦਾ ਹੈ ਜੋ ਜਦੋਂ ਇਲੈਕਟ੍ਰਿਕ ਕਰੰਟ ਇਸ ਵਿਚ ਵਹਿੰਦਾ ਹੈ ਤਾਂ ਇਸ ਦੁਆਰਾ ਚੁੰਬਕੀ ਕ੍ਸ਼ੇਤਰ ਦੇ ਰੂਪ ਵਿੱਚ ਊਰਜਾ ਸਟੋਰ ਕਰਦਾ ਹੈ। ਇਸਨੂੰ ਇੱਕ ਕੋਈਲ, ਚੋਕ ਜਾਂ ਰੀਅਕਟਰ ਵੀ ਕਿਹਾ ਜਾ ਸਕਦਾ ਹੈ।

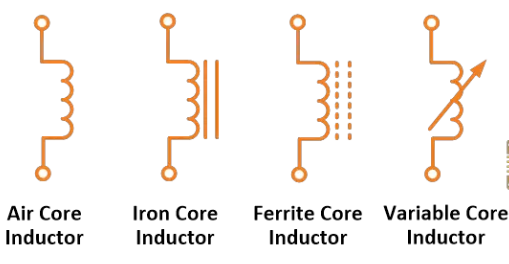
ਇੰਡਕਟਰ ਬਸ ਇੱਕ ਤਾਂਗਾ ਹੈ। ਇਹ ਆਮ ਤੌਰ 'ਤੇ ਇੱਕ ਕੋਈਲ ਦੇ ਰੂਪ ਵਿੱਚ ਹੋਣਗਾ ਜੋ ਇੱਕ ਪਲਾਸਟਿਕ ਜਾਂ ਫੇਰੋਮੈਗਨੈਟਿਕ ਸਾਮਗ੍ਰੀ ਦੇ ਇੱਕ ਲੋਹੇ ਦੇ ਕੋਰ ਵਿੱਚ ਲਿਪਟਿਆ ਹੋਇਆ ਹੋਵੇਗਾ; ਇਸ ਲਈ ਇਸਨੂੰ ਇੱਕ ਲੋਹੇ ਦਾ ਕੋਰ ਇੰਡਕਟਰ ਕਿਹਾ ਜਾਂਦਾ ਹੈ।

ਇੰਡਕਟਰ ਆਮ ਤੌਰ 'ਤੇ 1 µH (10-6 H) ਤੋਂ 20 H ਦੇ ਰੇਂਜ ਵਿੱਚ ਉਪਲਬਧ ਹੁੰਦੇ ਹਨ। ਬਹੁਤ ਸਾਰੇ ਇੰਡਕਟਰ ਕੋਈਲ ਦੇ ਅੰਦਰ ਫੇਰੀਟ ਜਾਂ ਲੋਹੇ ਦੇ ਇੱਕ ਚੁੰਬਕੀ ਕੋਰ ਨਾਲ ਬਣੇ ਹੁੰਦੇ ਹਨ, ਜੋ ਇਸਨੂੰ ਇੰਡਕਟਰ ਦੀ ਇੰਡਕਟੈਂਸ ਨੂੰ ਵਧਾਉਣ ਲਈ ਇਸਤੇਮਾਲ ਕੀਤਾ ਜਾਂਦਾ ਹੈ।

ਫਾਰਾਡੇ ਦੇ ਇਲੈਕਟ੍ਰੋਮੈਗਨੈਟਿਕ ਇੰਡਕਸ਼ਨ ਦੇ ਨਿਯਮ ਅਨੁਸਾਰ, ਜਦੋਂ ਇੰਡਕਟਰ ਜਾਂ ਕੋਈਲ ਦੀ ਵਿੱਚ ਵਹਿੰਦਾ ਹੋਣ ਵਾਲਾ ਇਲੈਕਟ੍ਰਿਕ ਕਰੰਟ ਬਦਲਦਾ ਹੈ, ਤਾਂ ਸਮੇਂ-ਵਿਵਰਣ ਚੁੰਬਕੀ ਕ੍ਸ਼ੇਤਰ ਇੱਕ e.m.f (ਇਲੈਕਟ੍ਰੋਮੋਟੀਵ ਫੋਰਸ) ਜਾਂ ਵੋਲਟੇਜ ਨੂੰ ਉਤਪਨਨ ਕਰਦਾ ਹੈ। ਇੰਡਕਟਰ ਦੇ ਵਿਚ ਪ੍ਰਵੇਸ਼ ਕੀਤੀ ਗਈ ਵੋਲਟੇਜ ਜਾਂ e.m.f. ਇੰਡਕਟਰ ਦੀ ਵਿੱਚ ਵਹਿੰਦੇ ਹੋਣ ਵਾਲੇ ਇਲੈਕਟ੍ਰਿਕ ਕਰੰਟ ਦੇ ਬਦਲਾਅ ਦੇ ਦਰ ਦੇ ਸਹਿਯੋਗੀ ਹੁੰਦੀ ਹੈ।

ਆਇੰਡਕਟੈਂਸ (L) ਇਕ ਆਇੰਡਕਟਰ ਦੀ ਇੱਕ ਵਿਸ਼ੇਸ਼ਤਾ ਹੈ ਜੋ ਇਸ ਦੁਆਰਾ ਪਾਸੇ ਹੋਣ ਵਾਲੀ ਧਾਰਾ ਦੇ ਮਾਤਰਾ ਜਾਂ ਦਿਸ਼ਾ ਵਿੱਚ ਬਦਲਾਅ ਦੀ ਵਿਰੋਧ ਕਰਦੀ ਹੈ। ਆਇੰਡਕਟਰ ਦੀ ਆਇੰਡਕਟੈਂਸ ਜਿਤਨੀ ਵੱਧ ਹੋਵੇਗੀ, ਉਤਨੀ ਹੀ ਇਹ ਮੈਗਨੈਟਿਕ ਫੀਲਡ ਦੇ ਰੂਪ ਵਿੱਚ ਵਿਦਿਵਾਨ ਊਰਜਾ ਸਟੋਰ ਕਰਨ ਦੀ ਕਸਮਤ ਵਧ ਜਾਵੇਗੀ।

ਆਇੰਡਕਟਰ ਕਿਵੇਂ ਕੰਮ ਕਰਦੇ ਹਨ?

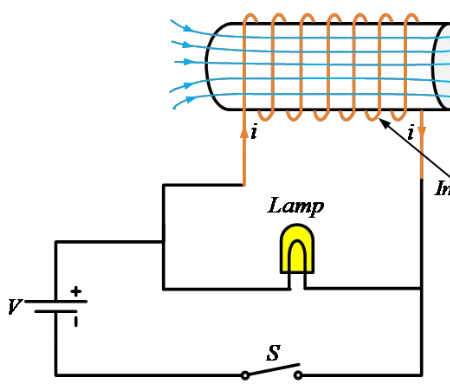
ਸਰਕਿਟ ਵਿੱਚ ਆਇੰਡਕਟਰ ਧਾਰਾ ਦੇ ਪਾਸੇ ਹੋਣ ਵਾਲੇ ਬਦਲਾਅ ਦੀ ਵਿਰੋਧ ਕਰਦਾ ਹੈ ਜਦੋਂ ਕਿ ਇਸ ਦੁਆਰਾ ਇੱਕ ਵੋਲਟੇਜ ਪ੍ਰਦਾਨ ਕੀਤਾ ਜਾਂਦਾ ਹੈ ਜੋ ਧਾਰਾ ਦੇ ਪਾਸੇ ਹੋਣ ਵਾਲੇ ਬਦਲਾਅ ਦੇ ਹਿੱਸੇ ਦੇ ਅਨੁਕੂਲ ਹੁੰਦਾ ਹੈ। ਇਹ ਸਮਝਣ ਲਈ ਕਿ ਆਇੰਡਕਟਰ ਸਰਕਿਟ ਵਿੱਚ ਕਿਵੇਂ ਕੰਮ ਕਰਦਾ ਹੈ, ਨੇੜੇ ਦਿੱਤੀ ਗਈ ਛਵੀ ਦੀ ਵਿਚਾਰ ਕਰੋ।

ਜਿਵੇਂ ਕਿ ਦਿਖਾਇਆ ਗਿਆ ਹੈ, ਇੱਕ ਲਾਂਭ, ਇੱਕ ਤਾਂਬੇ ਦਾ ਕੋਈਲ (ਆਇੰਡਕਟਰ), ਅਤੇ ਇੱਕ ਸਵਿਚ ਇੱਕ ਬੈਟਰੀ ਨਾਲ ਜੋੜੇ ਗਏ ਹਨ। ਜੇ ਅਸੀਂ ਸਰਕਿਟ ਤੋਂ ਆਇੰਡਕਟਰ ਨੂੰ ਹਟਾ ਦੇਂ, ਤਾਂ ਲਾਂਭ ਨੰਮਾਲ ਰੌਸ਼ਨ ਹੋ ਜਾਂਦਾ ਹੈ। ਆਇੰਡਕਟਰ ਨਾਲ, ਸਰਕਿਟ ਪੂਰੀ ਤਰ੍ਹਾਂ ਵੱਖਰਾ ਵਿਅਕਤੀ ਬਣ ਜਾਂਦਾ ਹੈ।

ਆਇੰਡਕਟਰ ਜਾਂ ਕੋਈਲ ਦਾ ਰੀਸਿਸਟੈਂਸ ਲਾਂਭ ਨਾਲ ਤੁਲਨਾ ਕੀਤੇ ਜਾਂਦੇ ਹੋਏ ਬਹੁਤ ਘੱਟ ਹੈ, ਇਸ ਲਈ ਜਦੋਂ ਸਵਿਚ ਬੰਦ ਕੀਤਾ ਜਾਂਦਾ ਹੈ ਤਾਂ ਸਭ ਤੋਂ ਵੱਧ ਧਾਰਾ ਕੋਈਲ ਦੇ ਰਾਹੀਂ ਪਾਸੇ ਹੋਵੇਗੀ ਕਿਉਂਕਿ ਇਹ ਧਾਰਾ ਲਈ ਇੱਕ ਘੱਟ ਰੀਸਿਸਟੈਂਸ ਦਾ ਰਾਹ ਪ੍ਰਦਾਨ ਕਰਦਾ ਹੈ। ਇਸ ਲਈ, ਅਸੀਂ ਲਾਂਭ ਨੂੰ ਬਹੁਤ ਘੱਟ ਰੌਸ਼ਨ ਹੋਣ ਦੀ ਉਮੀਦ ਕਰਦੇ ਹਾਂ।

ਪਰ ਆਇੰਡਕਟਰ ਦੀ ਵਿਅਕਤੀ ਕਾਰਨ, ਜਦੋਂ ਅਸੀਂ ਸਵਿਚ ਬੰਦ ਕਰਦੇ ਹਾਂ, ਤਾਂ ਲਾਂਭ ਰੌਸ਼ਨ ਹੋ ਜਾਂਦਾ ਹੈ ਅਤੇ ਫਿਰ ਘੱਟ ਰੌਸ਼ਨ ਹੋ ਜਾਂਦਾ ਹੈ ਅਤੇ ਜਦੋਂ ਅਸੀਂ ਸਵਿਚ ਖੋਲਦੇ ਹਾਂ, ਤਾਂ ਬਲਬ ਬਹੁਤ ਰੌਸ਼ਨ ਹੋ ਜਾਂਦਾ ਹੈ ਅਤੇ ਫਿਰ ਜਲਦੀ ਬੰਦ ਹੋ ਜਾਂਦਾ ਹੈ।

ਇਹ ਕਾਰਨ ਹੈ ਕਿ, ਜਦੋਂ ਆਇੰਡਕਟਰ ਦੇ ਦੋਵਾਂ ਪਾਸੇ ਵੋਲਟੇਜ ਜਾਂ ਵੋਲਟੇਜ ਦੇ ਅੰਤਰ ਲਾਗੁ ਕੀਤਾ ਜਾਂਦਾ ਹੈ, ਤਾਂ ਆਇੰਡਕਟਰ ਦੀ ਧਾਰਾ ਇੱਕ ਮੈਗਨੈਟਿਕ ਫੀਲਡ ਪੈਦਾ ਕਰਦੀ ਹੈ। ਇਹ ਮੈਗਨੈਟਿਕ ਫੀਲਡ ਫਿਰ ਆਇੰਡਕਟਰ ਵਿੱਚ ਇੱਕ ਪ੍ਰਵਾਹਿਤ ਵਿਦਿਵਾਨ ਧਾਰਾ ਪੈਦਾ ਕਰਦਾ ਹੈ ਪਰ ਇਸ ਦੀ ਪੋਲਾਰਿਟੀ ਉਲਟ ਹੁੰਦੀ ਹੈ, ਲੈਂਜ਼ ਦੇ ਨਿਯਮ ਅਨੁਸਾਰ।

ਇਹ ਪ੍ਰਵਾਹਿਤ ਧਾਰਾ ਮੈਗਨੈਟਿਕ ਫੀਲਡ ਦੇ ਕਾਰਨ ਧਾਰਾ ਵਿੱਚ ਕਿਸੇ ਵੀ ਬਦਲਾਅ, ਵਾਧਾ ਜਾਂ ਘਟਾਅ, ਦੀ ਵਿਰੋਧ ਕਰਨ ਦੀ ਕੋਸ਼ਿਸ਼ ਕਰਦੀ ਹੈ। ਜਦੋਂ ਮੈਗਨੈਟਿਕ ਫੀਲਡ ਬਣ ਜਾਂਦਾ ਹੈ, ਤਾਂ ਧਾਰਾ ਸਹੀ ਢੰਗ ਨਾਲ ਪਾਸੇ ਹੋ ਸਕਦੀ ਹੈ।

ਹੁਣ, ਜਦੋਂ ਸਵਿਚ ਬੰਦ ਕੀਤਾ ਜਾਂਦਾ ਹੈ, ਤਾਂ ਆਇੰਡਕਟਰ ਦੇ ਇਰਦੇ ਮੈਗਨੈਟਿਕ ਫੀਲਡ ਧਾਰਾ ਨੂੰ ਆਇੰਡਕਟਰ ਵਿੱਚ ਪਾਸੇ ਹੋਣ ਦੀ ਅਨੁਮਤੀ ਦੇਂਦਾ ਹੈ ਜਦੋਂ ਮੈਗਨੈਟਿਕ ਫੀਲਡ ਟੁੱਟ ਜਾਂਦਾ ਹੈ। ਇਹ ਧਾਰਾ ਲਾਂਭ ਨੂੰ ਕੁਝ ਸਮੇਂ ਤੱਕ ਰੌਸ਼ਨ ਰੱਖਦੀ ਹੈ ਭਾਵੇਂ ਸਵਿਚ ਖੋਲਿਆ ਗਿਆ ਹੋਵੇ।

ਇਹ ਇਸ ਪ੍ਰਕਾਰ ਕਿਹਾ ਜਾ ਸਕਦਾ ਹੈ ਕਿ, ਆਇੰਡਕਟਰ ਮੈਗਨੈਟਿਕ ਫੀਲਡ ਦੇ ਰੂਪ ਵਿੱਚ ਊਰਜਾ ਸਟੋਰ ਕਰ ਸਕਦਾ ਹੈ ਅਤੇ ਇਹ ਧਾਰਾ ਵਿੱਚ ਕਿਸੇ ਵੀ ਬਦਲਾਅ ਦੀ ਵਿਰੋਧ ਕਰਨ ਦੀ ਕੋਸ਼ਿਸ਼ ਕਰਦਾ ਹੈ। ਇਸ ਲਈ, ਇਸ ਦਾ ਪ੍ਰਾਥਮਿਕ ਨਤੀਜਾ ਯਹ ਹੈ ਕਿ ਆਇੰਡਕਟਰ ਦੀ ਧਾਰਾ ਤੁਰੰਤ ਬਦਲ ਨਹੀਂ ਸਕਦੀ।

ਆਇੰਡਕਟਰ ਸਰਕਿਟ ਸੰਕੇਤ

ਇੱਕ ਆਇੰਡਕਟਰ ਦਾ ਸ਼ੈਮਾਟਿਕ ਸਰਕਿਟ ਸੰਕੇਤ ਨੇੜੇ ਦਿੱਤੀ ਗਈ ਛਵੀ ਵਿੱਚ ਦਿਖਾਇਆ ਗਿਆ ਹੈ।

ਇੰਡੱਕਟਰ ਸਮੀਕਰਣ

ਇੰਡੱਕਟਰ ਦੇ ਉੱਤੇ ਵੋਲਟੇਜ਼

ਇੰਡੱਕਟਰ ਦੇ ਉੱਤੇ ਵੋਲਟੇਜ਼ ਇੱਕ ਦੁਆਰਾ ਬਿਜਲੀ ਦੇ ਵਹਿਣ ਦੀ ਦਰ ਨਾਲ ਸਹਿਯੋਗੀ ਹੈ। ਗਣਿਤਿਕ ਰੂਪ ਵਿੱਚ, ਇੰਡੱਕਟਰ ਦੇ ਉੱਤੇ ਵੋਲਟੇਜ਼ ਨੂੰ ਇਸ ਤਰ੍ਹਾਂ ਪ੍ਰਗਟ ਕੀਤਾ ਜਾ ਸਕਦਾ ਹੈ,

$\begin{align*} v_L = L \frac{di_L}{dt} \end{align*}$

ਜਿੱਥੇ, $v_L$ = ਇੰਡੱਕਟਰ ਦੇ ਉੱਤੇ ਤਿਵਾਨਾ ਵੋਲਟੇਜ਼ (ਵੋਲਟ ਵਿੱਚ),

$L$ = ਇੰਡੱਕਟੈਂਸ (ਹੈਨਰੀ ਵਿੱਚ),

$\frac{di_L}{dt}$ = ਬਿਜਲੀ ਦੀ ਵਹਿਣ ਦੀ ਦਰ (ਐਂਪੀਅਰ ਪ੍ਰਤੀ ਸਕਿੰਟ)

ਇੰਡਕਟਰ ਦੀ ਮੈਗਨੈਟਿਕ ਫੀਲਡ ਵਿੱਚ ਸਟੋਰ ਕੀਤੀ ਗਈ ਊਰਜਾ ਕਾਰਨ ਇੰਡਕਟਰ ਦੁਆਰਾ ਪ੍ਰਦਰਸ਼ਿਤ ਵੋਲਟੇਜ ਹੁੰਦਾ ਹੈ।

ਜੇਕਰ ਡੀਸੀ ਕਰੰਟ ਇੰਡਕਟਰ ਦੇ ਮੱਧਦ ਵਿੱਚ ਵਹਿੰਦੀ ਹੈ ਤਾਂ ਇੱਥੇ $\frac{di_L}{dt}$ ਸਮੇਂ ਦੀ ਨਿਸ਼ਚਿਤਤਾ ਦੇ ਕਾਰਨ ਸਹੀ ਹੋ ਜਾਂਦਾ ਹੈ ਅਤੇ ਇਸ ਲਈ ਇੰਡਕਟਰ ਦੁਆਰਾ ਪ੍ਰਦਰਸ਼ਿਤ ਵੋਲਟੇਜ ਸਿਫ਼ਰ ਹੋ ਜਾਂਦਾ ਹੈ। ਇਸ ਲਈ, ਜਿਵੇਂ ਡੀਸੀ ਮਾਤਰਾਵਾਂ ਦੀ ਪ੍ਰਤੀ ਵਿਚਾਰ ਕੀਤੀ ਜਾਂਦੀ ਹੈ, ਸਥਿਰ ਅਵਸਥਾ ਵਿੱਚ, ਇੰਡਕਟਰ ਇੱਕ ਸ਼ੋਰਟ ਸਰਕਿਟ ਦੀ ਤਰ੍ਹਾਂ ਕੰਮ ਕਰਦਾ ਹੈ।

ਇੰਡਕਟਰ ਦੀ ਵਿੱਚ ਵਹਿੰਦੀ ਕਰੰਟ

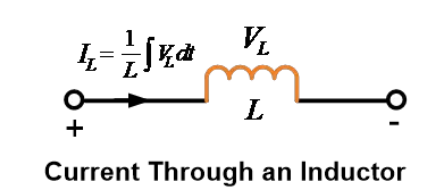
ਇੰਡਕਟਰ ਦੀ ਵਿੱਚ ਵਹਿੰਦੀ ਕਰੰਟ ਨੂੰ ਇਸ ਦੇ ਉੱਤੇ ਵਿਕਸਿਤ ਹੋਣ ਵਾਲੀ ਵੋਲਟੇਜ ਦੇ ਰੂਪ ਵਿੱਚ ਵਿਅਕਤ ਕੀਤਾ ਜਾ ਸਕਦਾ ਹੈ

$\begin{align*} i_L = \frac{1}{L} \int v_L dt \end{align*}$

ਉਪਰੋਕਤ ਸਮੀਕਰਣ ਵਿੱਚ, ਇਨਟੀਗਰੇਸ਼ਨ ਦੀਆਂ ਲਿਮਿਟਸ ਪਿਛਲੀ ਇਤਿਹਾਸ ਜਾਂ ਆਰੰਭਿਕ ਸਥਿਤੀਆਂ ਦੀ ਪ੍ਰਤੀ ਵਿਚਾਰ ਕਰਕੇ ਤਿਆਰ ਕੀਤੀਆਂ ਜਾਂਦੀਆਂ ਹਨ, ਯਾਨੀ ਸ਼ੁਰੂਆਤ $-\infty \,\, to \,\, t(0^-)$ ਤੋਂ।

ਹੁਣ, ਇਹ ਧਾਰਨਾ ਕਰਦੇ ਹੋਏ ਕਿ ਸਵਿਚਿੰਗ ਕਾਰਵਾਈ t=0 ਉੱਤੇ ਹੁੰਦੀ ਹੈ, ਇਹ ਮਤਲਬ ਹੈ ਕਿ ਸਵਿਚ t=0 ਉੱਤੇ ਬੰਦ ਹੁੰਦਾ ਹੈ। ਅਸੀਂ ਇੰਡਕਟਰ ਦੀ ਵਿੱਚ ਵਹਿੰਦੀ ਕਰੰਟ ਦਾ ਸਮੀਕਰਣ ਹੇਠ ਲਿਖਿਆ ਹੈ,

$\begin{align*} i_L = \frac{1}{L} \int v_L dt \end{align*}$

ਸਾਨੂੰ ਸ਼ੁੱਧ ਲਗਾਤ ਦੀਆਂ ਸੀਮਾਵਾਂ ਨੂੰ ਦੋ ਅੰਤਰਾਲਾਂ ਵਿਚ ਵੰਡ ਸਕਦੇ ਹਾਂ $-\infty \,\, to \,\, 0$ ਅਤੇ $0 \,\, to \,\,t$ । ਅਸੀਂ ਜਾਣਦੇ ਹਾਂ ਕਿ $0^-$ ਸਵਿੱਚਿੰਗ ਕਾਰਵਾਈ ਦੇ ਬਾਅਦ ਹੋਣ ਵਾਲੀ ਸਥਿਤੀ ਹੈ, ਜਦੋਂ ਕਿ $0^+$ ਸਵਿੱਚਿੰਗ ਕਾਰਵਾਈ ਦੇ ਪਹਿਲਾਂ ਹੋਣ ਵਾਲੀ ਸਥਿਤੀ ਹੈ। ਇਸ ਲਈ, ਅਸੀਂ ਲਿਖ ਸਕਦੇ ਹਾਂ

$\begin{align*} i_L = \frac{1}{L} \int_{-\infty}^{t} v_L dt \end{align*}$

ਇਸ ਲਈ,

$\begin{align*} i_L = \frac{1}{L} \int_{-\infty}^{0^-} v_L dt + \frac{1}{L} \int_{0^-}^{t} v_L dt \end{align*}$

ਇੱਥੇ, ਪਦ $\frac{1}{L} \int_{-\infty}^{0^-} v_L dt$ ਇਤਿਹਾਸਕ ਅਵਧੀ ਦੇ ਇੰਡਕਟਰ ਕਰੰਟ ਦਾ ਮੁੱਲ ਦਰਸਾਉਂਦਾ ਹੈ ਜੋ ਕਿ $i_L$ ਦੀ ਪ੍ਰਾਰੰਭਕ ਸਥਿਤੀ ਹੈ। ਇਸ ਨੂੰ $i_L(0^-)$ ਨਾਲ ਦਰਸਾਇਆ ਜਾਵੇ।

$\begin{align*} i_L = i_L(0^-) + \frac{1}{L} \int_{0^-}^{t} v_L dt \end{align*}$

ਤੇ $t=0^+$ , ਅਸੀਂ ਲਿਖ ਸਕਦੇ ਹਾਂ,

$\begin{align*} i_L (0^+)= i_L(0^-) + \frac{1}{L} \int_{0^-}^{0^+} v_L dt \end{align*}$

ਸ਼ੁਰੂਆਤ ਵਿੱਚ, ਅਸੀਂ ਮੰਨਿਆ ਕਿ ਸਵਿੱਚਿੰਗ ਕਾਰਵਾਈ ਜ਼ੀਰੋ ਸਮੇਂ 'ਤੇ ਹੁੰਦੀ ਹੈ। ਇਸ ਲਈ, ਇਨਟੈਗਰੇਸ਼ਨ $0^-$ ਤੋਂ $0^+$ ਤੱਕ ਸ਼ੁਣਿਆ ਹੈ।

ਇਸ ਲਈ,

$\begin{align*} i_L(0^-) = i_L(0^+) \end{align*}$

ਇਸ ਲਈ, ਇੰਡਕਟਰ ਦੀ ਧਾਰਾ ਤੁਰੰਤ ਬਦਲ ਨਹੀਂ ਸਕਦੀ। ਇਹ ਮਤਲਬ ਹੈ ਕਿ ਇੰਡਕਟਰ ਦੀ ਧਾਰਾ, ਸਵਿੱਚਿੰਗ ਕਾਰਵਾਈ ਤੋਂ ਪਹਿਲਾਂ ਅਤੇ ਬਾਅਦ ਵਿੱਚ ਇਕੱਠੀ ਹੈ।

ਇੰਡਕਟਰ ਜਦੋਂ t=0

ਆਇੰਡੱਕਟਰ ਦੀ ਸਥਿਤੀ ਵਿੱਚ $t = 0$ , ਜਿਵੇਂ ਕਿ ਆਇੰਡੱਕਟਰ ਉੱਤੇ ਵੋਲਟੇਜ ਸਵਿੱਚ ਕਰਨ ਦੀ ਸਥਿਤੀ ਵਿੱਚ, ਆਇਦੀਅਲ ਰੀਤੀ ਨਾਲ $\infty$ ਹੁੰਦੀ ਹੈ ਕਿਉਂਕਿ ਸਮੇਂ ਦੀ ਲੰਬਾਈ $dt$ ਸ਼ੂਨਿਅ ਹੁੰਦੀ ਹੈ। ਇਸ ਲਈ, ਸਵਿੱਚ ਕਰਨ ਦੀ ਸਥਿਤੀ ਵਿੱਚ ਆਇੰਡੱਕਟਰ ਖੁੱਲੇ ਸਰਕਿਟ ਦੀ ਤਰ੍ਹਾਂ ਕੰਮ ਕਰਦਾ ਹੈ। ਜਦੋਂ ਕਿ ਸਥਿਰ ਅਵਸਥਾ ਵਿੱਚ $t = \infty$ ਵਿੱਚ ਇਹ ਏਕ ਛੋਟੀ ਸਰਕਿਟ ਦੀ ਤਰ੍ਹਾਂ ਕੰਮ ਕਰਦਾ ਹੈ।

ਜੇਕਰ ਆਇੰਡੱਕਟਰ ਦੀ ਪਹਿਲਾਂ ਹੀ ਸਵਿੱਚ ਕਾਰਵਾਈ ਤੋਂ ਪਹਿਲਾਂ ਇੱਕ ਸ਼ੁਰੂਆਤੀ ਧਾਰਾ I0 ਹੈ, ਤਾਂ ਕਦੇ $t=0^+$ ਇਹ ਇੱਕ ਸਥਿਰ ਧਾਰਾ ਸਰਚ ਦੀ ਤਰ੍ਹਾਂ ਕੰਮ ਕਰਦਾ ਹੈ ਜਿਸਦਾ ਮੁੱਲ $I_0$ ਹੁੰਦਾ ਹੈ, ਜਦੋਂ ਕਿ ਸਥਿਰ ਅਵਸਥਾ ਵਿੱਚ $t=\infty$ ਵਿੱਚ, ਇਹ ਇੱਕ ਧਾਰਾ ਸਰਚ ਦੇ ਊਪਰ ਇੱਕ ਛੋਟੀ ਸਰਕਿਟ ਦੀ ਤਰ੍ਹਾਂ ਕੰਮ ਕਰਦਾ ਹੈ।

ਸੀਰੀਜ ਅਤੇ ਪੈਰਲੈਲ ਆਇੰਡੱਕਟਰਾਂ

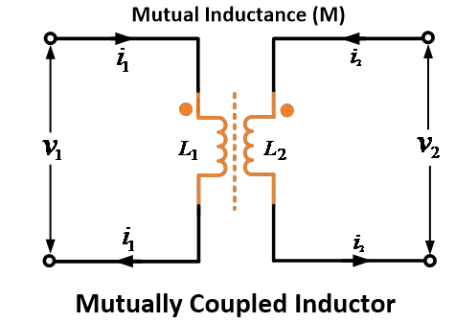
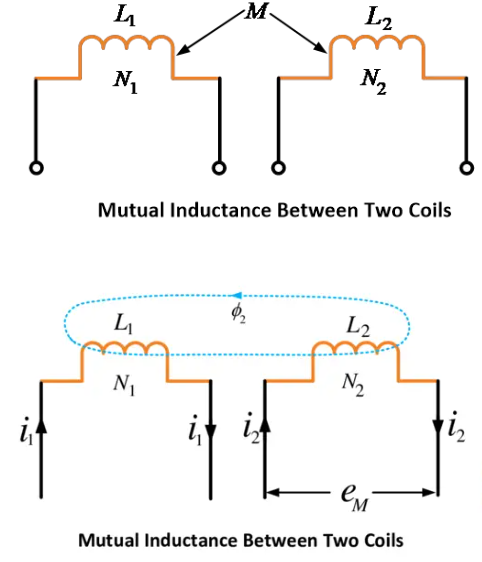
ਸੇਰੀ ਅਤੇ ਸਮਾਂਤਰ ਵਿੱਚ ਇੰਡਕਟਰ ਦਾ ਵਿਹਾਵ ਸੇਰੀ ਅਤੇ ਸਮਾਂਤਰ ਵਿੱਚ ਰੈਜਿਸਟਰ ਦੇ ਵਿਹਾਵ ਨਾਲ ਸਮਾਨ ਹੁੰਦਾ ਹੈ। ਦੋ ਮੈਗਨੈਟਿਕਲੀ ਕੌਪਲਡ ਕੋਲਾਂ 1 ਅਤੇ 2 ਦੀ ਵਿਚਾਰਨਾ ਜਿਨ੍ਹਾਂ ਦਾ ਸੈਲਫ-ਇੰਡਕਟੈਂਸ $L_1$ ਅਤੇ $L_2$ ਹੈ। ਮਾਨ ਲਓ ਕਿ ਦੋ ਕੋਲਾਂ ਦਰਮਿਆਨ ਮਿਉਟਿਊਅਲ ਇੰਡਕਟੈਂਸ M ਹੈ ਜੋ ਹੈਨਰੀ ਵਿੱਚ ਹੈ।

ਇਲੈਕਟ੍ਰਿਕ ਸਰਕਿਟ ਵਿਚ ਦੋ ਇੰਡਕਟਰ ਵਿੱਚ ਅਲਗ-ਅਲਗ ਤਰੀਕਿਆਂ ਨਾਲ ਜੋੜੇ ਜਾ ਸਕਦੇ ਹਨ ਜੋ ਬਦਲ ਵਿੱਚ ਬਦਲੇ ਬਦਲੇ ਸਮਾਨਕਾਰੀ ਇੰਡਕਟੈਂਸ ਦੇ ਮੁੱਲ ਦੇਣ ਲਈ ਹੁੰਦੇ ਹਨ ਜਿਵੇਂ ਹੇਠ ਚਰਚਾ ਕੀਤਾ ਗਿਆ ਹੈ।

ਸੇਰੀ ਵਿੱਚ ਇੰਡਕਟਰ ਦੀ ਫ਼ਾਰਮੂਲਾ

ਸੇਰੀ ਵਿੱਚ ਇੰਡਕਟਰ ਕਿਵੇਂ ਜੋੜੇ ਜਾਂਦੇ ਹਨ

ਦੋ ਪਾਰਸਪਰਿਕ ਕੌਪਲਡ ਇੰਡਕਟਰ ਜੋ ਸੇਰੀ ਵਿੱਚ ਜੋੜੇ ਗਏ ਹਨ ਵਾਲੇ ਸਰਕਿਟ ਦੀ ਵਿਚਾਰਨਾ ਕਰੋ। ਇੰਡਕਟਰ ਨੂੰ ਸੇਰੀ ਵਿੱਚ ਜੋੜਨ ਦੇ ਦੋ ਸੰਭਵ ਤਰੀਕੇ ਹਨ।

ਪਹਿਲੇ ਤਰੀਕੇ ਵਿੱਚ, ਇੰਡਕਟਰ ਦੁਆਰਾ ਉਤਪਾਦਿਤ ਫਲਾਕਸ ਇੱਕ ਹੀ ਦਿਸ਼ਾ ਵਿੱਚ ਕਾਰਯ ਕਰਦੇ ਹਨ। ਫਿਰ, ਇਹ ਇੰਡਕਟਰ ਸੇਰੀ-ਐਡਿੰਗ ਜਾਂ ਕੁਮੁਲੇਟਿਵ ਰੂਪ ਵਿੱਚ ਜੋੜੇ ਗਏ ਕਹਿਦੇ ਜਾਂਦੇ ਹਨ।
ਦੂਜੇ ਤਰੀਕੇ ਵਿੱਚ, ਜੇਕਰ ਇੱਕ ਇੰਡਕਟਰ ਵਿੱਚ ਕਰੰਟ ਉਲਟ ਕਰ ਦਿਆ ਜਾਂਦਾ ਹੈ ਤਾਂ ਕਿ ਇੰਡਕਟਰ ਦੁਆਰਾ ਉਤਪਾਦਿਤ ਫਲਾਕਸ ਆਪਸ ਵਿੱਚ ਵਿਰੋਧ ਕਰਦੇ ਹਨ, ਤਾਂ ਇਹ ਇੰਡਕਟਰ ਸੇਰੀ-ਅਪੋਜਿਸ਼ਨ ਜਾਂ ਡਿਫ੍ਰੈਂਸ਼ੀਅਲ ਰੂਪ ਵਿੱਚ ਜੋੜੇ ਗਏ ਕਹਿਦੇ ਜਾਂਦੇ ਹਨ।

ਲਿੰਡੂਕਟਰ 1 ਦਾ ਸਵ-ਅੱਧਾਨਕਤਾ $L_1$ ਅਤੇ ਲਿੰਡੂਕਟਰ 2 ਦਾ ਸਵ-ਅੱਧਾਨਕਤਾ $L_2$ । ਦੋਵਾਂ ਲਿੰਡੂਕਟਰ ਮੁਟੋਅਲ ਅੱਧਾਨਕਤਾ M ਨਾਲ ਜੋੜੇ ਹੋਏ ਹਨ।

ਸੀਰੀਜ ਸਹਾਇਕ (ਕਮੁਲੇਟਿਵ) ਕਨੈਕਸ਼ਨ (ਮੁਟੋਅਲ ਪ੍ਰਵਾਹਿਤ ਈਐਮਐਫ ਸਵ-ਪ੍ਰਵਾਹਿਤ ਈਐਮਐਫ ਨੂੰ ਸਹਾਇਕ ਬਣਾਉਂਦਾ ਹੈ)

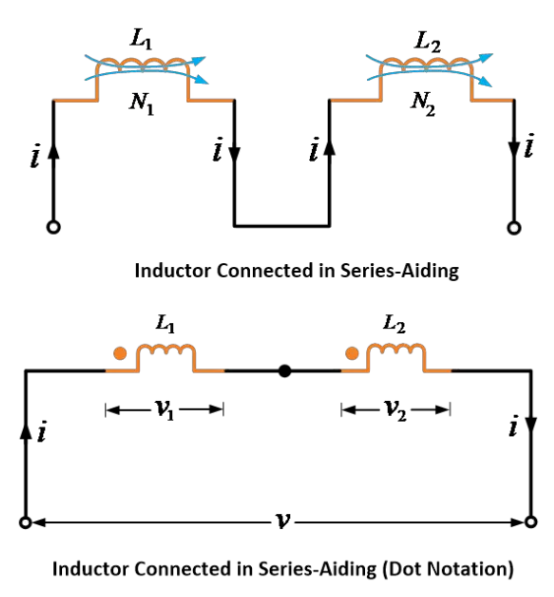
ਦੋ ਲਿੰਡੂਕਟਰ ਜਾਂ ਕੋਇਲ ਨੂੰ ਸੀਰੀਜ ਸਹਾਇਕ ਜਾਂ ਕਮੁਲੇਟਿਵ ਰੂਪ ਵਿੱਚ ਜੋੜਿਆ ਗਿਆ ਹੈ, ਜਿਵੇਂ ਨਿਚੇ ਦੀ ਛਬੀ ਵਿੱਚ ਦਿਖਾਇਆ ਗਿਆ ਹੈ।

ਇਸ ਕਨੈਕਸ਼ਨ ਵਿੱਚ, ਦੋਵਾਂ ਲਿੰਡੂਕਟਰਾਂ ਦਾ ਸਵ ਅਤੇ ਮੁਟੋਅਲ ਫਲਾਕਸ ਇਕੋ ਦਿਸ਼ਾ ਵਿੱਚ ਕਾਰਯ ਕਰਦਾ ਹੈ; ਇਸ ਲਈ, ਸਵ ਅਤੇ ਮੁਟੋਅਲ ਪ੍ਰਵਾਹਿਤ ਈਐਮਐਫ ਵੀ ਇਕੋ ਦਿਸ਼ਾ ਵਿੱਚ ਹੁੰਦੇ ਹਨ।

ਇਸ ਲਈ,

ਲਿੰਡੂਕਟਰ 1 ਵਿੱਚ ਸਵ-ਪ੍ਰਵਾਹਿਤ ਈਐਮਐਫ, $e_s_1 = -L_1\frac{di}{dt}$
ਲਿੰਡੂਕਟਰ 1 ਵਿੱਚ ਮੁਟੋਅਲ ਪ੍ਰਵਾਹਿਤ ਈਐਮਐਫ, $e_m_1 = -M\frac{di}{dt}$
ਲਿੰਡੂਕਟਰ 2 ਵਿੱਚ ਸਵ-ਪ੍ਰਵਾਹਿਤ ਈਐਮਐਫ, $e_s_2 = -L_2\frac{di}{dt}$
ਆਪਸ ਵਿੱਚ ਪ੍ਰਵਾਨ ਕੀਤਾ ਗਿਆ ਇ.ਮੈਲ.ਐੱਫ. ਇੰਡਕਟਰ 1 ਵਿੱਚ, $e_m_2 = -M\frac{di}{dt}$

ਸੰਯੁਕਤ ਇ.ਮੈਲ.ਐੱਫ. ਦੀ ਕੁੱਲ ਪ੍ਰਵਾਨ ਕੀਤੀ ਗਈ ਰਾਸ਼ੀ,

$\begin{align*} e=-(L_1\frac{di}{dt}+M\frac{di}{dt}+L_2\frac{di}{dt}+M\frac{di}{dt}) \end{align*}$

(1) $\begin{equation*} e = -(L_1+L_2+2M) \frac{di}{dt} \end{equation*}$

ਜੇਕਰ $L_eq$ ਦੋ ਇੰਡਕਟਰਾਂ ਦੀ ਸ਼੍ਰੇਣੀ ਵਿੱਚ ਸਹਾਇਕ ਸਥਿਤੀ ਵਿੱਚ ਸਮਝੋਤਾ ਇੰਡਕਟੈਂਸ ਹੈ, ਤਾਂ ਸੰਯੁਕਤ ਇੰਡਕਟੈਂਸ ਵਿੱਚ ਪ੍ਰਵਾਨ ਕੀਤੀ ਗਈ ਇ.ਮੈਲ.ਐੱਫ. ਇਸ ਦੁਆਰਾ ਦਿੱਤੀ ਜਾਂਦੀ ਹੈ,

(2) $\begin{equation*} e = -L_e_q_. \frac{di}{dt} \end{equation*}$

ਸਮੀਕਰਣ (1) ਅਤੇ (2) ਨੂੰ ਤੁਲਨਾ ਕਰਦੇ ਹੋਏ, ਅਸੀਂ ਪ੍ਰਾਪਤ ਕਰਦੇ ਹਾਂ,

(3) $\begin{equation*} L_e_q_. = L_1 + L_2 + 2M \end{equation*}$

ਉੱਪਰਲੀ ਸਮੀਕਰਣ ਦੋ ਕ੍ਰਮਵਾਰ ਜੋੜੇ ਗਏ ਅਤੇ ਜੋੜਦਾਰ ਕੁਨਡਾਂ ਦੀ ਸਮਾਨਕਾਲੀ ਆਵੇਸ਼ਾਂਕਤਾ ਦਿੰਦੀ ਹੈ।

ਜੇਕਰ ਦੋਵਾਂ ਕੁਨਡਾਂ ਦੇ ਬੀਚ ਕੋਈ ਪਾਰਸਪਰਿਕ ਆਵੇਸ਼ਾਂਕਤਾ ਨਹੀਂ ਹੈ (ਭਾਵ, M = 0), ਤਾਂ,

$\begin{align*} L_e_q_. = L_1 + L_2 \end{align*}$

ਸੀਰੀਜ ਵਿਰੋਧ (ਅੰਤਰ) ਕਨੈਕਸ਼ਨ (ਪਾਰਸਪਰਿਕ ਰੂਪ ਵਿੱਚ ਉੱਤਪਾਦਿਤ ਈਐਮਐਫ ਆਤਮਕ ਉੱਤਪਾਦਿਤ ਈਐਮਐਫ ਦੀ ਵਿਰੋਧੀ ਹੈ)

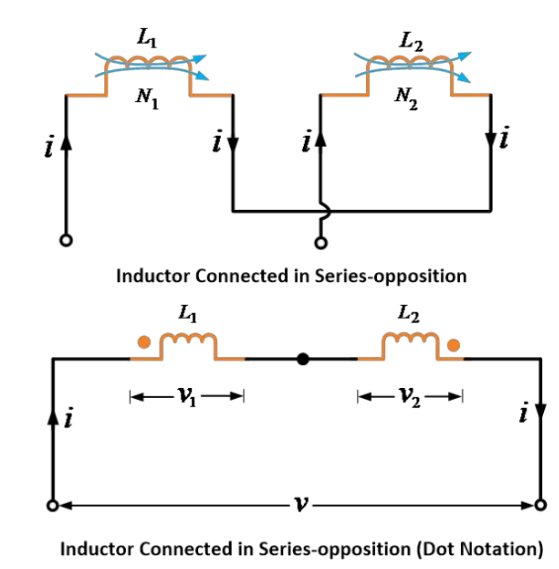
ਇੱਕ ਸਰਕਿਟ ਦਾ ਵਿਚਾਰ ਕਰੋ ਜਿਸ ਵਿੱਚ ਦੋ ਪਾਰਸਪਰਿਕ ਜੋੜੇ ਗਏ ਆਵੇਸ਼ਾਂਕਤਾ ਜਾਂ ਕੁਨਡੇ ਕ੍ਰਮਵਾਰ ਜੋੜੇ ਗਏ ਹਨ ਤਾਂ ਕਿ ਦੋਵਾਂ ਆਵੇਸ਼ਾਂਕਤਾ ਦੁਆਰਾ ਉੱਤਪਾਦਿਤ ਫਲਾਕਸ ਆਪਸ ਨੂੰ ਵਿਰੋਧ ਕਰਦੇ ਹਨ, ਜਿਵੇਂ ਨੀਚੇ ਦੀ ਛਬੀ ਵਿੱਚ ਦਰਸਾਇਆ ਗਿਆ ਹੈ।

ਜੇਕਰ ਫਲਾਕਸ ਵਿਰੋਧ ਵਿੱਚ ਹਨ, ਤਾਂ ਪਾਰਸਪਰਿਕ ਰੂਪ ਵਿੱਚ ਉੱਤਪਾਦਿਤ ਈਐਮਐਫ ਦਾ ਚਿਹਨ ਆਤਮਕ ਉੱਤਪਾਦਿਤ ਈਐਮਐਫ ਦੇ ਵਿਰੋਧ ਵਿੱਚ ਹੋਵੇਗਾ। ਇਸ ਲਈ,

ਆਤਮਕ ਉੱਤਪਾਦਿਤ ਈਐਮਐਫ ਆਵੇਸ਼ਾਂਕਤਾ 1 ਵਿੱਚ, $e_s_1 = -L_1\frac{di}{dt}$
ਇੰਡੱਕਟਰ 1 ਵਿੱਚ ਪਰਸਪਰ ਉੱਤਪਨ ਹੋਣ ਵਾਲਾ ਈ.ਐਮ.ਐੱਫ., $e_m_1 = +M\frac{di}{dt}$
ਇੰਡੱਕਟਰ 2 ਵਿੱਚ ਆਤਮਕ ਉੱਤਪਨ ਹੋਣ ਵਾਲਾ ਈ.ਐਮ.ਐੱਫ., $e_s_2 = -L_2\frac{di}{dt}$
ਇੰਡੱਕਟਰ 2 ਵਿੱਚ ਪਰਸਪਰ ਉੱਤਪਨ ਹੋਣ ਵਾਲਾ ਈ.ਐਮ.ਐੱਫ., $e_m_2 = +M\frac{di}{dt}$

ਯੋਜਨਾ ਵਿੱਚ ਉੱਤਪਨ ਹੋਣ ਵਾਲਾ ਕੁੱਲ ਈ.ਐਮ.ਐੱਫ.,

$\begin{align*} e=-(L_1\frac{di}{dt}-M\frac{di}{dt}+L_2\frac{di}{dt}-M\frac{di}{dt}) \end{align*}$

(4) $\begin{equation*} e = -(L_1+L_2-2M) \frac{di}{dt} \end{equation*}$

ਜੇਕਰ $L_e_q$ ਦੋਵਾਂ ਇੰਡੱਕਟਰਾਂ ਦਾ ਸ਼੍ਰੇਣੀ ਵਿਰੋधੀ ਸ਼ਲਾਗਾਂਤਰ ਸੰਚਾਲਨ ਵਿੱਚ ਸਮਾਨਕ ਇੰਡੱਕਟੈਂਸ ਹੈ, ਤਾਂ ਯੋਜਨਾ ਵਿੱਚ ਉੱਤਪਨ ਹੋਣ ਵਾਲਾ ਈ.ਐਮ.ਐੱਫ. ਦਿੱਤਾ ਗਿਆ ਹੈ,

(੫) $\begin{equation*} e = -L_e_q_. \frac{di}{dt} \end{equation*}$

ਸਮੀਕਰਣ (੪) ਅਤੇ (੫) ਨੂੰ ਤੁਲਨਾ ਕਰਦੇ ਹੋਏ, ਅਸੀਂ ਪ੍ਰਾਪਤ ਕਰਦੇ ਹਾਂ,

(੬) $\begin{equation*} L_e_q_. = L_1 + L_2 - 2 M \end{equation*}$

ਉੱਤੇ ਦਿੱਤਾ ਗਿਆ ਸਮੀਕਰਣ ਦੋ ਆਇਨਡੈਕਟਰਾਂ ਨੂੰ ਸ਼੍ਰੇਣੀ ਵਿੱਚ ਵਿਰੋਧੀ ਜੋੜਦਿਆਂ ਜਾਂ ਅੰਤਰਨਾਲਿਕ ਜੋੜ ਦੇ ਤੌਰ 'ਤੇ ਜੋੜਦਿਆਂ ਦਾ ਸਮਾਨ ਆਇਨਡੈਕਟੈਂਸ ਦਿੰਦਾ ਹੈ।

ਜੇਕਰ ਦੋਵਾਂ ਕੋਲਾਂ ਦੇ ਬੀਚ ਕੋਈ ਮਿਲਦਾਰ ਆਇਨਡੈਕਟੈਂਸ ਨਹੀਂ ਹੈ (ਜਿਵੇਂ ਕਿ, M = ੦), ਤਾਂ,

$\begin{align*} L_e_q_. = L_1 + L_2 \end{align*}$

ਉਦਾਹਰਣ ੧

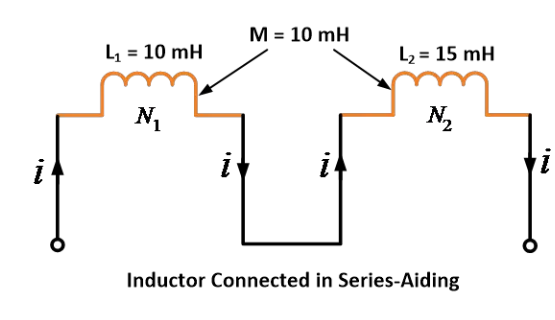
ਦੋ ਕੋਲਾਂ ਦਾ ਸਵਲੰਬ ਆਇਨਡੈਕਟੈਂਸ ੧੦ ਮਿਲੀਹੈਂਰੀ ਅਤੇ ੧੫ ਮਿਲੀਹੈਂਰੀ ਹੈ ਅਤੇ ਦੋਵਾਂ ਕੋਲਾਂ ਦੇ ਬੀਚ ਮਿਲਦਾਰ ਆਇਨਡੈਕਟੈਂਸ ੧੦ ਮਿਲੀਹੈਂਰੀ ਹੈ। ਜਦੋਂ ਇਹ ਸ਼੍ਰੇਣੀ ਵਿੱਚ ਸਹਾਇਕ ਜੋੜ ਹੋਣ ਤੇ ਸਮਾਨ ਆਇਨਡੈਕਟੈਂਸ ਪਤਾ ਕਰੋ।

ਹੱਲ:

ਦਿੱਤੀਆਂ ਗਈਆਂ ਸੰਖਿਆਵਾਂ: L1 = 10 mH, L2 = 15 mH ਅਤੇ M = 10 mH

ਸੀਰੀਜ ਆਡ ਕਰਨ ਦੀ ਵਿਧੀ ਅਨੁਸਾਰ,

$\begin{align*} \begin{split} & L_e_q_. = L_1 + L_2 + 2M \\ & = 10 + 15 + 2(10) \\ & = 10 + 15 + 20 \\ & L_e_q_. = 45\,\,mH \end{split} \end{align*}$

ਇਸ ਲਈ, ਸਮੀਕਰਣ ਦੀ ਵਰਤੋਂ ਕਰਕੇ, ਜਦੋਂ ਉਹ ਸੀਰੀਜ ਆਡ ਕੀਤੇ ਜਾਂਦੇ ਹਨ, ਤਾਂ ਸਮਾਨਕ ਆਦਾਨਕਤਾ 45 mH ਪ੍ਰਾਪਤ ਹੁੰਦੀ ਹੈ।

ਉਦਾਹਰਨ 2

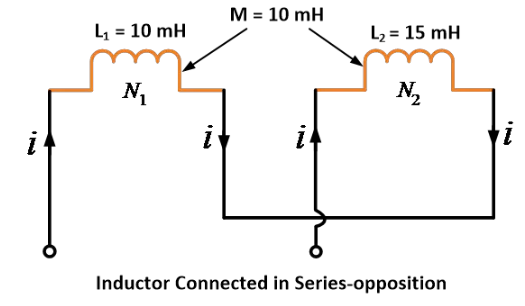
ਦੋ ਕੋਈਲਾਂ ਦੀਆਂ ਸਵ-ਆਦਾਨਕਤਾਵਾਂ 10 mH ਅਤੇ 15 mH ਹਨ ਅਤੇ ਦੋਵਾਂ ਕੋਈਲਾਂ ਦੀ ਮਿਲਦੀ ਆਦਾਨਕਤਾ 10 mH ਹੈ। ਜਦੋਂ ਉਹ ਸੀਰੀਜ ਵਿਰੋਧ ਕੀਤੇ ਜਾਂਦੇ ਹਨ, ਤਾਂ ਸਮਾਨਕ ਆਦਾਨਕਤਾ ਪਤਾ ਕਰੋ।

ਹੱਲ:

ਦਿੱਤੀਆਂ ਗਈਆਂ ਸੰਖਿਆਵਾਂ: L1 = 10 mH, L2 = 15 mH ਅਤੇ M = 10 mH

ਸੀਰੀਜ ਵਿਰੋਧ ਦੀ ਵਿਧੀ ਅਨੁਸਾਰ,

$\begin{align*} \begin{split} & L_e_q_. = L_1 + L_2 - 2M \\ & = 10 + 15 - 2(10) \\ & = 10 + 15 - 20 \\ & = 25 - 20 \\ & L_e_q_. = 5\,\,mH \end{split} \end{align*}$

ਇਸ ਲਈ, ਸਮੀਕਰਣ ਦੀ ਵਰਤੋਂ ਕਰਦੇ ਹੋਏ ਅਸੀਂ ਉਨ੍ਹਾਂ ਨੂੰ ਸ਼੍ਰੇਣੀ ਵਿੱਚ ਵਿਰੋਧੀ ਢੰਗ ਨਾਲ ਜੋੜਦੇ ਵਕਤ 5 mH ਦੀ ਬਰਾਬਰੀ ਆਪਣੀ ਪ੍ਰਾਪਤ ਕਰਦੇ ਹਾਂ।

ਸਮਾਂਤਰ ਵਿੱਚ ਇੰਡੱਕਟਰਾਂ ਦਾ ਸੂਤਰ

ਸਮਾਂਤਰ ਵਿੱਚ ਇੰਡੱਕਟਰਾਂ ਨੂੰ ਕਿਵੇਂ ਜੋੜਣਾ ਹੈ

ਦੋ ਇੰਡੱਕਟਰਾਂ ਨੂੰ ਇਸ ਤਰ੍ਹਾਂ ਸਮਾਂਤਰ ਵਿੱਚ ਜੋੜਿਆ ਜਾ ਸਕਦਾ ਹੈ ਕਿ

ਤਾਲਮੇਲੀ ਉਤਪਨ ਕੀਤੀ ਈਏਐਮਐਫ ਆਤਮਕ ਉਤਪਨ ਕੀਤੀ ਈਏਐਮਐਫ ਨੂੰ ਸਹਾਇਕ ਕਰਦੀ ਹੈ, ਜਿਹੜਾ ਕਿ ਸਮਾਂਤਰ ਸਹਾਇਕ ਜੋੜਾਂ ਦਾ ਸੰਲਗਨ ਹੈ
ਤਾਲਮੇਲੀ ਉਤਪਨ ਕੀਤੀ ਈਏਐਮਐਫ ਆਤਮਕ ਉਤਪਨ ਕੀਤੀ ਈਏਐਮਐਫ ਨੂੰ ਵਿਰੋਧੀ ਕਰਦੀ ਹੈ, ਜਿਹੜਾ ਕਿ ਸਮਾਂਤਰ ਵਿਰੋਧੀ ਜੋੜਾਂ ਦਾ ਸੰਲਗਨ ਹੈ

ਸਮਾਂਤਰ-ਸਹਾਇਕ (ਇਕੱਠਾ ਕਰਨ ਵਾਲਾ) ਜੋੜਾ (ਤਾਲਮੇਲੀ ਉਤਪਨ ਕੀਤੀ ਈਏਐਮਐਫ ਆਤਮਕ ਉਤਪਨ ਕੀਤੀ ਈਏਐਮਐਫ ਨੂੰ ਸਹਾਇਕ ਕਰਦੀ ਹੈ)

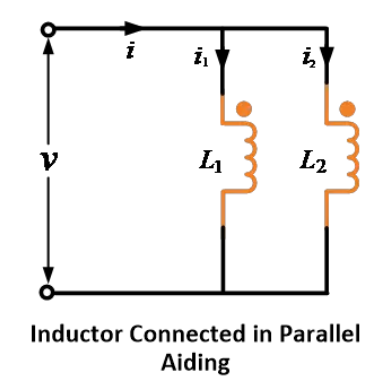
ਜਦੋਂ ਦੋ ਇੰਡੱਕਟਰਾਂ ਨੂੰ ਸਮਾਂਤਰ ਸਹਾਇਕ ਤੌਰ 'ਤੇ ਜੋੜਿਆ ਜਾਂਦਾ ਹੈ, ਤਾਂ ਤਾਲਮੇਲੀ ਉਤਪਨ ਕੀਤੀ ਈਏਐਮਐਫ ਆਤਮਕ ਉਤਪਨ ਕੀਤੀ ਈਏਐਮਐਫ ਨੂੰ ਸਹਾਇਕ ਕਰਦੀ ਹੈ, ਜਿਵੇਂ ਨੀਚੇ ਦੀ ਫਿਗਰ ਵਿੱਚ ਦਿਖਾਇਆ ਗਿਆ ਹੈ।

ਇੰਡੱਕਟਰਾਂ L₁ ਅਤੇ L₂ ਦੇ ਮੁੱਖ ਵਿੱਚ ਵਹਿਣ ਵਾਲੀਆਂ ਵਿੱਤੀਆਂ i₁ ਅਤੇ i₂ ਦੇ ਸਾਥ I ਸਾਰੀ ਵਿੱਤੀ ਹੈ।

ਇਸ ਲਈ,

(7) $\begin{equation*} i = i_1 + i_2 \end{equation*}$

ਇਸ ਲਈ,

(8) $\begin{equation*} \frac{di}{dt} = \frac{di_1}{dt} + \frac{di_2}{dt} \end{equation*}$

ਹਰ ਇੰਡੱਕਟਰ ਵਿੱਚ ਦੋ ਈਐਮਐਫੀਜ਼ ਪੈਦਾ ਹੋਣਗੀਆਂ। ਇਕ ਸਵਲਫ ਇੰਡੱਕਸ਼ਨ ਤੋਂ ਅਤੇ ਦੂਜੀ ਮਿਊਚੁਅਲ ਇੰਡੱਕਸ਼ਨ ਤੋਂ।

ਇੰਡੱਕਟਰ ਸਮਾਂਤਰ ਰੀਤੀ ਨਾਲ ਜੋੜੇ ਹਨ, ਇਸ ਲਈ ਈਐਮਐਫੀਜ਼ ਬਰਾਬਰ ਹਨ।

ਇਸ ਲਈ,

(9) $\begin{equation*} L_1 \frac{di_1}{dt} + M \frac{di_2}{dt} = L_2 \frac{di_2}{dt} + M \frac{di_1}{dt} \end{equation*}$

$\begin{align*} L_1 \frac{di_1}{dt} - M \frac{di_1}{dt} = L_2 \frac{di_2}{dt} - M \frac{di_2}{dt} \end{align*}$

$\begin{align*} \frac{di_1}{dt} (L_1 - M) = \frac{di_2}{dt} (L_2 - M) \end{align*}$

(10) $\begin{equation*} \frac{di_1}{dt} = (\frac{L_2 - M}{L_1 - M}) \frac{di_2}{dt} \end{equation*}$

ਹੁਣ, ਸਮੀਕਰਨ (9) ਨੂੰ ਸਮੀਕਰਨ (8) ਵਿਚ ਪੁੱਟਦੇ ਹਾਂ, ਅਸੀਂ ਪ੍ਰਾਪਤ ਕਰਦੇ ਹਾਂ,

$\begin{align*} \frac{di}{dt} = (\frac{L_2 - M}{L_1 - M}) \frac{di_2}{dt} + \frac{di_2}{dt} \end{align*}$

(੧੧) $\begin{equation*} \frac{di}{dt} = (1 + \frac{L_2 - M}{L_1 - M}) + \frac{di_2}{dt} \end{equation*}$

ਜੇਕਰ $L_e_q.$ ਸਮਾਂਤਰ ਜੋੜੀਆਂ ਦੇ ਇੰਡੱਕਟਰਾਂ ਦੀ ਸਮਾਨ ਇੰਡੱਕਟੈਂਸ ਹੈ, ਤਾਂ ਇਸ ਵਿਚ ਪ੍ਰਵਾਹਿਤ ਹੋਣ ਵਾਲਾ ਏਮਐਫ ਹੋਵੇਗਾ

(੧੨) $\begin{equation*} e = L_e_q_. \frac{di}{dt} \end{equation*}$

ਇਹ ਕਿਸੇ ਵੀ ਇੱਕ ਕੋਈਲ ਵਿਚ ਪ੍ਰਵਾਹਿਤ ਹੋਣ ਵਾਲੇ ਏਮਐਫ ਦੇ ਬਰਾਬਰ ਹੈ, ਅਰਥਾਤ,

$\begin{align*} L_e_q_. \frac{di}{dt} = L_1 \frac{di_1}{dt} + M \frac{di_2}{dt} \end{align*}$

(13) $\begin{equation*} \frac{di}{dt} = \frac{1}{L_e_q_.} [L_1 \frac{di_1}{dt} + M \frac{di_2}{dt}] \end{equation*}$

ਸਮੀਕਰਣ (10) ਵਿੱਚੋਂ $\frac{di_1}{dt}$ ਦਾ ਮੁੱਲ ਸਮੀਕਰਣ (13) ਵਿੱਚ ਰੱਖਣ 'ਤੇ ਪ੍ਰਾਪਤ ਹੁੰਦਾ ਹੈ,

$\begin{align*} \frac{di}{dt} = \frac{1}{L_e_q_.} [L_1 (\frac{L_2 - M}{L_1 - M}) \frac{di_2}{dt} + M \frac{di_2}{dt}] \end{align*}$

(14) $\begin{equation*} \frac{di}{dt} = \frac{1}{L_e_q_.} [L_1 (\frac{L_2 - M}{L_1 - M}) + M] \frac{di_2}{dt} \end{equation*}$

ਹੁਣ, ਸਮੀਕਰਣ (11) ਨੂੰ ਸਮੀਕਰਣ (14) ਨਾਲ ਬਰਾਬਰ ਕਰਨ 'ਤੇ,

$\begin{align*} 1+(\frac{L_2 - M}{L_1 - M}) \frac{di_2}{dt} = \frac{1}{L_e_q_.}[L_1 (\frac{L_2 - M}{L_1 - M}) + M]\frac{di_2}{dt} \end{align*}$

$\begin{align*} \frac{L_1+L_2 - 2M}{L_1 - M} = \frac{1}{L_e_q_.} [\frac{L_1L_2- L_1M+L_1M - M^2}{L_1 - M}] \end{align*}$

$\begin{align*} \frac{L_1+L_2 - 2M}{L_1 - M} = \frac{1}{L_e_q_.} [\frac{L_1L_2 - M^2}{L_1 - M}] \end{align*}$

(15) $\begin{equation*} L_e_q_. = \frac{L_1L_2 - M^2}{L_1+L_2 - 2M} \end{equation*}$

ਉੱਪਰਲੀ ਸਮੀਕਰਣ ਦੋ ਇੰਡੱਕਟਰਾਂ ਨੂੰ ਪਾਰਲਲ-ਆਇਡਿੰਗ ਜਾਂ ਕੁਲਤ੍ਰਿਵ ਕਨੈਕਸ਼ਨ ਵਿਚ ਜੋੜਦਾ ਹੈ।

ਜੇ ਦੋਵਾਂ ਕੋਲਾਂ ਵਿਚਕਾਰ ਕੋਈ ਪਾਰਸਪਰਿਕ ਇੰਡੱਕਟੈਂਸ ਨਹੀਂ ਹੈ (ਅਰਥਾਤ, M = 0), ਤਾਂ,

$\begin{align*} L_e_q_. = \frac{L_1L_2 - (0)^2}{L_1+L_2-2(0)} = \frac{L_1L_2}{L_1+L_2} = \frac{product}{sum} \end{align*}$

ਸਮਾਂਤਰ ਵਿਰੋਧ (ਅੰਤਰ) ਸੰਲਗਨ (ਪਰਸਪਰ ਪ੍ਰਵਾਹੀਤ ਵੋਲਟੇਜ ਆਤਮਕ ਪ੍ਰਵਾਹੀਤ ਵੋਲਟੇਜਾਂ ਦੇ ਵਿਰੋਧ ਕਰਦਾ ਹੈ)

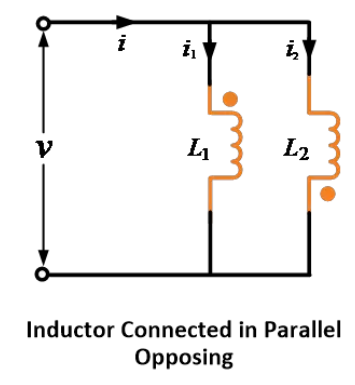
ਜਦੋਂ ਦੋ ਇੰਡਕਟਾਰ ਸਮਾਂਤਰ ਵਿਰੋਧ ਵਿਚ ਜੋੜੇ ਜਾਂਦੇ ਹਨ, ਤਾਂ ਪਰਸਪਰ ਪ੍ਰਵਾਹੀਤ ਵੋਲਟੇਜ ਆਤਮਕ ਪ੍ਰਵਾਹੀਤ ਵੋਲਟੇਜਾਂ ਦੇ ਵਿਰੋਧ ਕਰਦਾ ਹੈ।

ਹੇਠ ਦਿੱਤੀ ਛਬੀ ਵਿਚ ਦਿਖਾਇਆ ਗਿਆ ਹੈ ਕਿ ਦੋ ਇੰਡਕਟਾਰ ਸਮਾਂਤਰ ਵਿਰੋਧ ਜਾਂ ਅੰਤਰ ਵਿਚ ਜੋੜੇ ਗਏ ਹਨ।

ਸਮਾਂਤਰ-ਸਹਾਇਕ ਸੰਲਗਨ ਦੇ ਸਮਾਨ ਢੰਗ ਨਾਲ, ਇਹ ਸਿੱਧ ਕੀਤਾ ਜਾ ਸਕਦਾ ਹੈ ਕਿ,

(16) $\begin{equation*} L_e_q_. = \frac{L_1L_2 - M^2}{L_1+L_2 + 2M} \end{equation*}$

ਉੱਤੇ ਦਿੱਤੀ ਸਮੀਕਰਣ ਦੁਆਲੇ ਇੰਡਕਟਾਰ ਦੇ ਸਮਾਂਤਰ ਵਿਰੋਧ ਜਾਂ ਅੰਤਰ ਸੰਲਗਨ ਦਾ ਸਮਾਨ ਇੰਡਕਟਾਂਸ ਦਿੰਦੀ ਹੈ।

ਜੇਕਰ ਦੋ ਕੋਈਲਾਂ ਵਿਚੋਂ ਬੀਚ ਕੋਈ ਪਰਸਪਰ ਇੰਡਕਟਾਂਸ ਨਹੀਂ ਹੈ (ਭਾਵ, M = 0), ਤਾਂ,

$\begin{align*} L_e_q_. = \frac{L_1L_2 - (0)^2}{L_1+L_2+2(0)} = \frac{L_1L_2}{L_1+L_2} = \frac{product}{sum} \end{align*}$

ਉਦਾਹਰਣ 1

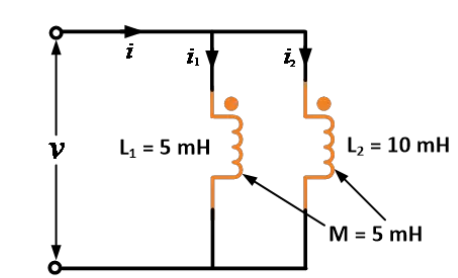
ਦੋ ਇੰਡੱਕਟਰ ਦੀਆਂ ਸਵ-ਇੰਡੱਕਟੈਂਸ਼ਨ 5 mH ਅਤੇ 10 mH ਹਨ ਅਤੇ ਦੋਵਾਂ ਵਿਚ ਪਾਰਸਪਰਿਕ ਇੰਡੱਕਟੈਂਸ਼ਨ 5 mH ਹੈ। ਜਦ ਇਹ ਸਮਾਂਤਰ ਰੂਪ ਵਿਚ ਜੋੜੇ ਜਾਂਦੇ ਹਨ, ਤਾਂ ਸਮਾਨਕਾਰੀ ਇੰਡੱਕਟੈਂਸ਼ਨ ਪਤਾ ਕਰੋ।

ਹੱਲ:

ਦਿੱਤੀਆਂ ਗਈਆਂ ਗਿਣਤੀਆਂ: L1 = 5 mH, L2 = 10 mH ਅਤੇ M = 5 mH

ਸਮਾਨਕਾਰੀ ਸਮੀਕਰਣ ਅਨੁਸਾਰ,

$\begin{align*} \begin{split} & L_e_q_. = \frac{L_1 L_2 - M^2}{L_1 + L_2 - 2M}.... if \,\, fluxes \,\, aid \\ & = \frac{5 * 10 - (5)^2}{5 + 10 - 2(5)} \\ & = \frac{50 - 25}{15 - 10} \\ & = \frac{25}{5} \\ & L_e_q_. = 5\,\,mH \end{split} \end{align*}$

ਇਸ ਤਰ੍ਹਾਂ, ਸਮੀਕਰਣ ਦੀ ਵਰਤੋਂ ਕਰਦੇ ਹੋਏ, ਜਦ ਇਹ ਸਮਾਂਤਰ ਰੂਪ ਵਿਚ ਜੋੜੇ ਜਾਂਦੇ ਹਨ, ਤਾਂ ਸਮਾਨਕਾਰੀ ਇੰਡੱਕਟੈਂਸ਼ਨ 5 mH ਪ੍ਰਾਪਤ ਹੁੰਦੀ ਹੈ।

ਉਦਾਹਰਣ 2

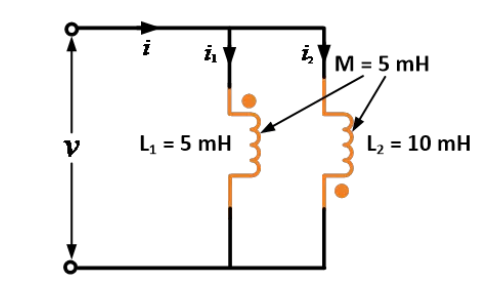
ਦੋ ਇੰਡੱਕਟਰਾਂ ਦੀਆਂ ਸਵ-ਇੰਡੱਕਟੈਂਸ਼ਨਾਂ ਦੀ ਗਿਣਤੀ 5 mH ਅਤੇ 10 mH ਹੈ ਅਤੇ ਦੋਵਾਂ ਵਿਚਕਾਰ ਮਿਉਤੀ ਇੰਡੱਕਟੈਂਸ਼ਨ 5 mH ਹੈ। ਜਦੋਂ ਉਹ ਸਹਾਇਕ ਵਿਰੋਧੀ ਬਣਾਏ ਜਾਂਦੇ ਹਨ ਤਾਂ ਸਮਾਨਤਾ ਪ੍ਰਦਾਨ ਕਰਨ ਵਾਲੀ ਇੰਡੱਕਟੈਂਸ਼ਨ ਲੱਭੋ।

ਹੱਲ:

ਦਿੱਤੀ ਗਈ ਗਿਣਤੀ: L1 = 5 mH, L2 = 10 mH ਅਤੇ M = 5 mH

ਸਹਾਇਕ ਵਿਰੋਧੀ ਫਾਰਮੁਲੇ ਅਨੁਸਾਰ,

$\begin{align*} \begin{split} & L_e_q_. = \frac{L_1 L_2 - M^2}{L_1 + L_2 + 2M}.... if \,\, fluxes \,\, oppose \\ & = \frac{5 * 10 - (5)^2}{5 + 10 + 2(5)} \\ & = \frac{50 - 25}{15 + 10} \\ & = \frac{25}{25} \\ & L_e_q_. = 1\,\,mH \end{split} \end{align*}$

ਇਸ ਲਈ, ਇਕੁਏਸ਼ਨ ਦੀ ਵਰਤੋਂ ਕਰਦੇ ਹੋਏ, ਜਦੋਂ ਉਹ ਸਹਾਇਕ ਵਿਰੋਧੀ ਬਣਾਏ ਜਾਂਦੇ ਹਨ ਤਾਂ ਸਮਾਨਤਾ ਪ੍ਰਦਾਨ ਕਰਨ ਵਾਲੀ ਇੰਡੱਕਟੈਂਸ਼ਨ 1 mH ਪ੍ਰਾਪਤ ਹੁੰਦੀ ਹੈ।

ਜੋੜੀਦਾਰ ਇੰਡੱਕਟਰਾਂ

ਜਦੋਂ ਇੱਕ ਇੰਡੱਕਟਰ (ਕੋਇਲ) ਦਾ ਚੁੰਬਕੀ ਕ਷ੇਤਰ ਇੱਕ ਹੋਰ ਪਾਸੇ ਦੇ ਇੰਡੱਕਟਰ ਦੀਆਂ ਪਾਲਾਂ ਨੂੰ ਕੱਟਦਾ ਹੈ ਜਾਂ ਲਿੰਕ ਕਰਦਾ ਹੈ, ਤਾਂ ਦੋਵਾਂ ਇੰਡੱਕਟਰਾਂ ਨੂੰ ਚੁੰਬਕੀ ਰੂਪ ਵਿੱਚ ਜੋੜੀਦਾਰ ਕਿਹਾ ਜਾਂਦਾ ਹੈ। ਜੋੜੀਦਾਰ ਇੰਡੱਕਟਰਾਂ ਕਰਕੇ, ਦੋਵਾਂ ਕੋਇਲਾਂ ਵਿਚ ਇੱਕ ਮਿਉਤੀ ਇੰਡੱਕਟੈਂਸ਼ਨ ਮੌਜੂਦ ਹੁੰਦੀ ਹੈ।

ਜੋੜੀਦਾਰ ਸਰਕਿਟਾਂ ਵਿੱਚ, ਜਦੋਂ ਕੋਈ ਵੀ ਸਰਕਿਟ ਊਰਜਾ ਸਹਾਰਾ ਕਰਦਾ ਹੈ, ਤਾਂ ਊਰਜਾ ਦਾ ਹੱਥਲੀ ਹੋਂਦਾ ਹੈ। ਇੱਕ ਦੋ-ਵਿਕਾਰ ਟ੍ਰਾਂਸਫਾਰਮਰ, ਇੱਕ ਑ਟੋਟ੍ਰਾਂਸਫਾਰਮਰ, ਅਤੇ ਇੱਕ ਇੰਡੱਕਸ਼ਨ ਮੋਟਰ ਚੁੰਬਕੀ ਜੋੜੀਦਾਰ ਇੰਡੱਕਟਰਾਂ ਜਾਂ ਕੋਇਲਾਂ ਜਾਂ ਸਰਕਿਟਾਂ ਦੇ ਉਦਾਹਰਣ ਹਨ।

ਦੋ ਮੈਗਨੈਟਿਕ ਰੂਪ ਵਿੱਚ ਜੋੜੇ ਹੋਏ ਇੰਡੱਕਟਰਜ਼ ਜਾਂ ਕੋਲਾਂ 1 ਅਤੇ 2 ਦੀ ਧਿਆਨ ਦਿਓ ਜਿਨ੍ਹਾਂ ਦੀਆਂ ਇੰਡੱਕਟੈਂਸ L₁ ਅਤੇ L₂ ਹੈ। ਦੋਵਾਂ ਕੋਲਾਂ ਵਿਚਕਾਰ ਮਿਉਟੁਅਲ ਇੰਡੱਕਟੈਂਸ M ਹੈ।

ਮਿਉਟੁਅਲ ਇੰਡੱਕਟੈਂਸ ਦਾ ਪ੍ਰਭਾਵ ਦੋਵਾਂ ਕੋਲਾਂ ਦੀ ਇੰਡੱਕਟੈਂਸ ਨੂੰ ਬਾਧਾ ਯਾਹਿਰਾਵ ਕਰਨ ਦਾ ਹੈ (L₁ + M ਅਤੇ L₂ + M) ਜਾਂ ਘਟਾਉਣ ਦਾ ਹੈ (L₁ – M ਅਤੇ L₂ – M), ਇਹ ਦੋਵਾਂ ਕੋਲਾਂ ਜਾਂ ਇੰਡੱਕਟਰਾਂ ਦੀ ਸਥਿਤੀ 'ਤੇ ਨਿਰਭਰ ਕਰਦਾ ਹੈ।

ਜੇਕਰ ਦੋ ਕੋਲਾਂ ਇਸ ਤਰ੍ਹਾਂ ਸਥਾਪਿਤ ਕੀਤੀਆਂ ਜਾਂਦੀਆਂ ਹਨ ਕਿ ਉਨ੍ਹਾਂ ਦੇ ਫਲਾਕਸ ਆਪਸ ਵਿਚ ਮਿਲਦੇ ਹਨ, ਤਾਂ ਹਰ ਕੋਲ ਦੀ ਇੰਡੱਕਟੈਂਸ M ਦੁਆਰਾ ਵਧ ਜਾਂਦੀ ਹੈ, ਜਿਹੜਾ ਕਿ L₁ + M ਕੋਲ 1 ਲਈ ਅਤੇ L₂ + M ਕੋਲ 2 ਲਈ ਹੁੰਦਾ ਹੈ। ਇਹ ਇਸ ਲਈ ਹੁੰਦਾ ਹੈ ਕਿ ਹਰ ਕੋਲ ਨਾਲ ਜੋੜੇ ਹੋਏ ਕੁਲ ਫਲਾਕਸ ਉਸ ਦੇ ਆਪਣੇ ਫਲਾਕਸ ਤੋਂ ਵੱਧ ਹੁੰਦੇ ਹਨ।
ਜੇਕਰ ਦੋ ਕੋਲਾਂ ਇਸ ਤਰ੍ਹਾਂ ਸਥਾਪਿਤ ਕੀਤੀਆਂ ਜਾਂਦੀਆਂ ਹਨ ਕਿ ਉਨ੍ਹਾਂ ਦੇ ਫਲਾਕਸ ਆਪਸ ਵਿਚ ਵਿਰੋਧੀ ਹੁੰਦੇ ਹਨ, ਤਾਂ ਹਰ ਕੋਲ ਦੀ ਇੰਡੱਕਟੈਂਸ M ਦੁਆਰਾ ਘਟ ਜਾਂਦੀ ਹੈ, ਜਿਹੜਾ ਕਿ L₁ – M ਕੋਲ 1 ਲਈ ਅਤੇ L₂ – M ਕੋਲ 2 ਲਈ ਹੁੰਦਾ ਹੈ। ਇਹ ਇਸ ਲਈ ਹੁੰਦਾ ਹੈ ਕਿ ਹਰ ਕੋਲ ਨਾਲ ਜੋੜੇ ਹੋਏ ਕੁਲ ਫਲਾਕਸ ਉਸ ਦੇ ਆਪਣੇ ਫਲਾਕਸ ਤੋਂ ਘੱਟ ਹੁੰਦੇ ਹਨ।

ਮਿਉਟੁਅਲ ਇੰਡੱਕਟੈਂਸ ਫਾਰਮੁਲਾ

ਅਸੀਂ ਜਾਣਦੇ ਹਾਂ ਕਿ ਕਿਸੇ ਇੱਕ ਕੋਲ ਵਿਚ ਕਰੰਟ ਦੀ ਕੋਈ ਵਿਕਾਸ ਹਮੇਸ਼ਾ ਦੂਜੇ ਕੋਲ ਵਿਚ ਮਿਉਟੁਅਲੀ ਇੰਡੱਕਟ ਕੀਤੀ ਈ.ਐਮ.ਐੱਫ. ਦੁਆਰਾ ਪੂਰਾ ਕੀਤਾ ਜਾਂਦਾ ਹੈ।

ਮਿਉਟੁਅਲ ਇੰਡੱਕਟੈਂਸ ਕਿਸੇ ਇੱਕ ਕੋਲ (ਜਾਂ ਸਰਕਿਟ) ਦੀ ਕ੍ਸਮ ਦੀ ਪਰਿਭਾਸ਼ਾ ਹੈ ਜੋ ਕਿਸੇ ਨੇੜੇ ਦੇ ਕੋਲ (ਜਾਂ ਸਰਕਿਟ) ਵਿਚ ਈ.ਐਮ.ਐੱਫ. ਦੁਆਰਾ ਇੰਡੱਕਸ਼ਨ ਦੁਆਰਾ ਉਤਪਾਦਨ ਕਰਦਾ ਹੈ ਜਦੋਂ ਪਹਿਲੇ ਕੋਲ ਵਿਚ ਕਰੰਟ ਦੀ ਕੋਈ ਵਿਕਾਸ ਹੁੰਦੀ ਹੈ।

ਹੋਰ ਸ਼ਬਦਾਂ ਵਿਚ, ਦੋ ਕੋਲਾਂ ਦੀ ਐਸੀ ਪ੍ਰੋਪਰਟੀ ਜਿਸ ਦੁਆਰਾ ਪ੍ਰਤਿ ਕੋਈ ਇੱਕ ਕੋਲ ਦੁਸਰੇ ਕੋਲ ਵਿਚ ਵਹਿਣ ਵਾਲੇ ਕਰੰਟ ਦੀ ਕੋਈ ਵਿਕਾਸ ਨੂੰ ਵਿਰੋਧ ਕਰਦਾ ਹੈ, ਇਸ ਨੂੰ ਦੋਵਾਂ ਕੋਲਾਂ ਦੀ ਮਿਉਟੁਅਲ ਇੰਡੱਕਟੈਂਸ ਕਿਹਾ ਜਾਂਦਾ ਹੈ। ਇਹ ਵਿਰੋਧ ਇਸ ਲਈ ਹੁੰਦਾ ਹੈ ਕਿ ਕਿਸੇ ਇੱਕ ਕੋਲ ਵਿਚ ਕਰੰਟ ਦੀ ਕੋਈ ਵਿਕਾਸ ਦੂਜੇ ਕੋਲ ਵਿਚ ਮਿਉਟੁਅਲੀ ਇੰਡੱਕਟ ਕੀਤੀ ਈ.ਐਮ.ਐੱਫ. ਦੁਆਰਾ ਪੈਦਾ ਹੁੰਦਾ ਹੈ ਜੋ ਪਹਿਲੇ ਕੋਲ ਵਿਚ ਕਰੰਟ ਦੀ ਵਿਕਾਸ ਨੂੰ ਵਿਰੋਧ ਕਰਦਾ ਹੈ।

ਮਿਉਟੁਅਲ ਇੰਡੱਕਟੈਂਸ (M) ਕੋਲ ਦੇ ਫਲਾਕਸ-ਲਿੰਕੇਜ਼ ਦੀ ਪ੍ਰਤੀ ਇਕਾਈ ਕਰੰਟ ਦੀ ਦੂਜੀ ਕੋਲ ਵਿਚ ਪਰਿਭਾਸ਼ਾ ਕੀਤੀ ਜਾ ਸਕਦੀ ਹੈ।

ਗਣਿਤਕ ਰੂਪ ਵਿੱਚ,

$\begin{align*} M = \frac{N_2 \phi_1_2}{I_1} \end{align*}$

ਜਿੱਥੇ,

$I_1$ = ਪਹਿਲੀ ਕੋਲ ਵਿਚ ਦਰਿਆ

$\phi_1_2$ = ਦੂਜੀ ਕੋਲ ਨਾਲ ਜੋੜੀ ਫਲਾਕਸ

$N_2$ = ਦੂਜੀ ਕੋਲ ਦੀਆਂ ਪੁੱਛਾਂ ਦੀ ਸੰਖਿਆ

ਦੋ ਕੋਲਾਂ ਦੀ ਪਾਰਸਪਰਿਕ ਆਇਨਡੈਕਸ਼ਨ 1 ਹੈਨਰੀ ਹੈ ਜੇਕਰ ਇੱਕ ਕੋਲ ਵਿੱਚ 1 ਐਮੀਅਰ ਪ੍ਰਤੀ ਸਕਾਂਦ ਦੇ ਰੇਟ ਨਾਲ ਬਦਲਦੀ ਹੋਣ ਵਾਲੀ ਦਰਿਆ ਦੁਜੀ ਕੋਲ ਵਿੱਚ 1 ਵੋਲਟ ਦੀ ਇੰਡਿਊਸਡ ਈ.ਐਮ.ਐੱਫ. ਲਈ ਹੈ।

ਕੁਪਲਿੰਗ ਦਾ ਗੁਣਾਂਕ

ਦੋ ਕੋਲਾਂ ਦੀ ਵਿਚ ਕੁਪਲਿੰਗ ਦਾ ਗੁਣਾਂਕ (k) ਇੱਕ ਕੋਲ ਵਿਚ ਦਰਿਆ ਦੁਆਰਾ ਉਤਪਨ ਕੀਤੀ ਹੋਣ ਵਾਲੀ ਮੈਗਨੈਟਿਕ ਫਲਾਕਸ ਦੀ ਹਿੱਸਾ ਦੇ ਰੂਪ ਵਿੱਚ ਪਰਿਭਾਸ਼ਿਤ ਹੈ ਜੋ ਦੂਜੀ ਕੋਲ ਨਾਲ ਜੋੜੀ ਹੈ।

ਕੁਪਲਿੰਗ ਦਾ ਗੁਣਾਂਕ ਕੁਪਲ ਸਰਕਟਾਂ ਲਈ ਇੱਕ ਮਹੱਤਵਪੂਰਨ ਪ੍ਰਾਮਾਣਿਕ ਸੰਖਿਆ ਹੈ ਜੋ ਉਦਘਾਟਕ ਰੂਪ ਨਾਲ ਕੁਪਲਿੱਤ ਕੋਲਾਂ ਦੀ ਵਿਚ ਕੁਪਲਿੰਗ ਦੀ ਮਾਤਰਾ ਨੂੰ ਨਿਰਧਾਰਿਤ ਕਰਦਾ ਹੈ।

ਗਣਿਤ ਦੇ ਅਨੁਸਾਰ, ਕੁਪਲਿੰਗ ਦਾ ਗੁਣਾਂਕ ਇਸ ਤਰ੍ਹਾਂ ਪ੍ਰਗਟ ਕੀਤਾ ਜਾ ਸਕਦਾ ਹੈ,

$\begin{align*} k = \frac{M}{\sqrt{L_1L_2}} \end{align*}$

ਜਿੱਥੇ,

L1 ਪਹਿਲੇ ਕੋਲ ਦਾ ਸਵਲਾਈਕ ਆਇਨਡੈਕਟੈਂਸ ਹੈ

L2 ਦੂਜੇ ਕੋਲ ਦਾ ਸਵਲਾਈਕ ਆਇਨਡੈਕਟੈਂਸ ਹੈ

M ਦੋਵਾਂ ਕੋਲਾਂ ਦੇ ਬੀਚ ਮਿਲਦਾਰ ਆਇਨਡੈਕਟੈਂਸ ਹੈ

ਕੁਪਲਿੰਗ ਗੁਣਾਂਕ ਦੋਵਾਂ ਕੋਲਾਂ ਦੇ ਬੀਚ ਮਿਲਦਾਰ ਆਇਨਡੈਕਟੈਂਸ 'ਤੇ ਨਿਰਭਰ ਕਰਦਾ ਹੈ। ਜੇ ਕੁਪਲਿੰਗ ਗੁਣਾਂਕ ਵਧੇ ਤਾਂ ਮਿਲਦਾਰ ਆਇਨਡੈਕਟੈਂਸ ਵੀ ਵਧੇਗਾ। ਦੋ ਉਦਘਾਟਕ ਰੂਪ ਨਾਲ ਕੁਪਲਿੱਤ ਕੋਲਾਂ ਨੂੰ ਚੁੰਬਕੀ ਫਲਾਕਸ ਦੀ ਵਰਤੋਂ ਨਾਲ ਜੋੜਿਆ ਜਾਂਦਾ ਹੈ।

ਜੇ ਇੱਕ ਕੋਲ ਦਾ ਪੂਰਾ ਫਲਾਕਸ ਦੂਜੇ ਕੋਲ ਨਾਲ ਲਿੰਕ ਹੋਏ ਤਾਂ ਕੁਪਲਿੰਗ ਦਾ ਗੁਣਾਂਕ 1 (ਅਰਥਾਤ 100%) ਹੁੰਦਾ ਹੈ, ਤਦ ਕੋਲ ਘਣੀ ਰੀਤੀ ਨਾਲ ਕੁਪਲਿੱਤ ਕਿਹਾ ਜਾਂਦਾ ਹੈ।
ਜੇ ਇੱਕ ਕੋਲ ਦਾ ਕੇਵਲ ਆਧਾ ਫਲਾਕਸ ਦੂਜੇ ਕੋਲ ਨਾਲ ਲਿੰਕ ਹੋਏ ਤਾਂ ਕੁਪਲਿੰਗ ਦਾ ਗੁਣਾਂਕ 0.5 (ਅਰਥਾਤ 50%) ਹੁੰਦਾ ਹੈ, ਤਦ ਕੋਲ ਢੀਲੀ ਰੀਤੀ ਨਾਲ ਕੁਪਲਿੱਤ ਕਿਹਾ ਜਾਂਦਾ ਹੈ।
ਜੇ ਇੱਕ ਕੋਲ ਦਾ ਫਲਾਕਸ ਦੂਜੇ ਕੋਲ ਨਾਲ ਕੋਈ ਲਿੰਕ ਨਾ ਹੋਵੇ ਤਾਂ ਕੁਪਲਿੰਗ ਦਾ ਗੁਣਾਂਕ 0 ਹੁੰਦਾ ਹੈ, ਤਦ ਕੋਲ ਚੁੰਬਕੀ ਰੂਪ ਨਾਲ ਅਲਗ ਕਿਹਾ ਜਾਂਦਾ ਹੈ।

ਕੁਪਲਿੰਗ ਦਾ ਗੁਣਾਂਕ ਹਮੇਸ਼ਾ ਇਕ ਤੋਂ ਘਟ ਹੋਵੇਗਾ। ਇਹ ਉਸ ਕੋਰ ਦੇ ਸਾਮਗ੍ਰੀ 'ਤੇ ਨਿਰਭਰ ਕਰਦਾ ਹੈ ਜਿਸ ਦੀ ਵਰਤੋਂ ਕੀਤੀ ਜਾਂਦੀ ਹੈ। ਹਵਾ ਦੇ ਕੋਰ ਲਈ, ਕੁਪਲਿੰਗ ਗੁਣਾਂਕ 0.4 ਤੋਂ 0.8 ਤੱਕ ਹੋ ਸਕਦਾ ਹੈ ਜੋ ਦੋ ਕੋਲਾਂ ਦੇ ਬੀਚ ਦੇ ਸਪੇਸ 'ਤੇ ਨਿਰਭਰ ਕਰਦਾ ਹੈ ਅਤੇ ਲੋਹੇ ਜਾਂ ਫੈਰਾਇਟ ਕੋਰ ਲਈ ਇਹ 0.99 ਤੱਕ ਹੋ ਸਕਦਾ ਹੈ।

ਸੋਟਾ: Electrical4u.

ਵਚਨ: ਅਸਲੀ ਨੂੰ ਸਹਿਯੋਗ ਦਿਓ, ਅਚ੍ਛੇ ਲੇਖ ਸਹਾਇਕ ਹਨ, ਜੇ ਕੋਈ ਉਲਾਘ ਹੋਵੇ ਤਾਂ ਕੰਟੈਕਟ ਕਰਕੇ ਮਿਟਾਓ।