سری او پارالل لګونه (فرمول او مثالونه)

فیلد: د اساسي برقو د خواصو

China

د اینډکټر څه دی؟

د اینډکټر (په همدا د اېلکټریکي اینډکټر په نوم) دوه ترمینلي دی چې د پاسيف اېلکټریکي المان په توګه دی چې د مغناطیسي فیلد شکل کې د انرژۍ لخوا د وړاندې کولو لپاره کارول کیږي، هغه وخت چې د ایلکټریکي جريان له هغه ځمکه وروسته راوړل کیږي. دا هم د کویل، چوک یا ریکټر په نوم دی.

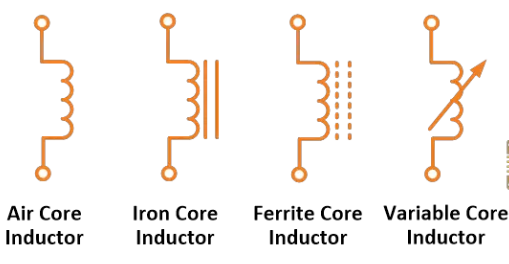
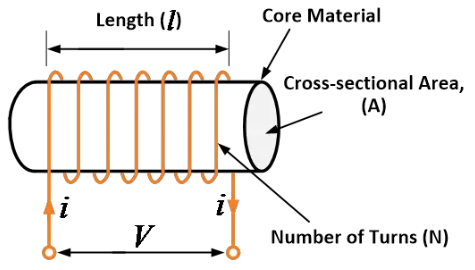
د اینډکټر ساده د کویل دی. دا معمولاً د کویل د دې چې د کنډکټر مواد، معمولاً د کاپر، د یک ډول پلاستیک یا فروماگنتیک مواد په څیر کې د یرون کور یا د فېروماغنیتیک مواد کور وړاندې کیږي؛ پسې د دې د نومونه د یرون کوری اینډکټر دی.

د اینډکټرونه معمولاً د ۱ µH (۱۰-6 H) تر ۲۰ H پورې موجود دي. زهات د اینډکټرونو د کور یا د فېروماغنیتیک مواد یا د لوړو کور یې د کویل کې داخل کیږي، چې دا د مغناطیسي فیلد او د اینډکټر د اینډکتانس زیاتولو لپاره کارول کیږي.

د فارادی لای قانون په توګه، هغه وخت چې د اینډکټر یا کویل کې د اېلکټریکي جريان بدلېږي، د وخت څخه متغیر مغناطیسي فیلد د e.m.f (الکتروموټیو فورس) یا ولټیج پیدا کوي. د اینډکټر ترمنځ د e.m.f یا ولټیج د اېلکټریکي جريان د بدلولو د درجې سره تناسب لري.

انډکتانس (L) د انډکټر يوه خصوصیت دی چې په دې کې تغییراتو ته مخالفت ورکوي. انډکټر جوړه شوی دی، دا د مغناطيسي میدان په توګه برقی انرژي ننګول کولو لپاره د کمک ورکوي.

د انډکټرونه څو څو ورکوي؟

د انډکټر په سیمینو کې د ځایونو او د کورنۍ تغییراتو ته مخالفت ورکوي، د دې ترمنځ د اړیکې د ځایونو تغییراتو په توګه ولولو سره. د انډکټر په سیمینو کې کوم ډول ورکوي، د لاندې وښیلو جوړښت په پام کې نیولو سره.

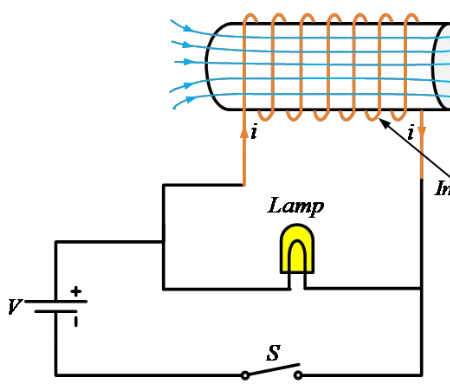
واخلم، د لنډنۍ، د تل یو سیمه (انډکټر)، او د کلیچ یو کلیچ په بټری کې وړاندې شوي دي. که د انډکټر په سیمینو کې دې، د لنډنۍ لوستل کېږي. د انډکټر سره، د سیمینو راځیعونه کاملاً مختلف وي.

د انډکټر یا د تل په پرتله د لنډنۍ سره د داونده له لږه دی. په دې توګه که د کلیچ بند شي، د کورنۍ زه د تل په پرتله لوی شته ورکوي. په دې توګه، د لنډنۍ د لوستل کېږي.

که د کلیچ بند شي، د لنډنۍ د لوستل کېږي او په دې توګه د کورنۍ د تل په پرتله لوی شته ورکوي. په دې توګه، د لنډنۍ د لوستل کېږي.

دلایل د دې ده چې که د ولولو یا د اختلاف ولولو د انډکټر په وړاندې کې ورکول شي، د کورنۍ په انډکټر کې د مغناطيسي میدان جوړه کوي. دا مغناطيسي میدان د انډکټر په توګه د لوی کورنۍ ولولو جوړه کوي.

دا لوی کورنۍ د مغناطيسي میدان په توګه د کورنۍ تغییراتو ته مخالفت ورکوي. که د مغناطيسي میدان جوړه شي، د کورنۍ طبیعي توګه ورکول شي.

که د کلیچ بند شي، د مغناطيسي میدان د کورنۍ په انډکټر کې د کورنۍ ورکول ته معاون وي. دا د لنډنۍ د لوستل کېږي.

د بل عبارت د دې د نتیجه ده چې د انډکټر په کورنۍ کې د کورنۍ د تغییراتو ته مخالفت ورکوي. په دې توګه، د کورنۍ په انډکټر کې د تغییراتو ته مخالفت ورکوي.

د انډکټر سیمینو سمبل

د انډکټر د سیمینو سمبل په لاندې وښیلو کې وړاندې شوی دی.

د اینډکټر معادله

د اینډکټر په وړاندې ولټیژ

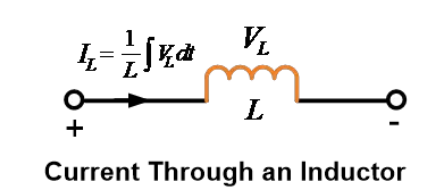
د اینډکټر په وړاندې ولټیژ د دې په وړاندې بېلابېلو کې د الکټریکي جريانونو د تیرېدونو توپیر سره متناسب دی. ریاضيي توګه، د اینډکټر په وړاندې ولټیژ په دې توګه نښته کیږي،

$\begin{align*} v_L = L \frac{di_L}{dt} \end{align*}$

که، $v_L$ = د اینډکټر په وړاندې لحظي ولټیژ (ولټ)،

$L$ = د هنري واحد (هنري) د اینډکټنس،

$\frac{di_L}{dt}$ = د الکټریکي جريانونو د تیرېدونو د دېروالی (امپیر په ثانیې کې)

د انډوکټر په سرونه کې د ولتاژ ارزښت د هغه د مغناطيسي چاودنې په داخل کې ذخیره شوي انرژي ته اړه لري.

که d.c. current د انډوکټر له لارې تېر شي، نو $\frac{di_L}{dt}$ صفر ته ورسوي ځکه چې d.c. جريان د وخت له مخې ثابت دی. په دې توګه، د انډوکټر په سرونه کې د ولتاژ ارزښت صفر ته ورسوي. نو، تر هغه چې d.c. کميتونه په ګورو، د حالت د ثبات په حال کې، انډوکټر د يو کوتولو سرتي سرکت په توګه عمل کوي.

جريان د يو انډوکټر له لارې

زموږ کولای شو چې د انډوکټر له لارې جريان بيا ويليکو په داسې ډول چې د هغې سره تړلې ولتاژ په اساس وي، لکه:

$\begin{align*} i_L = \frac{1}{L} \int v_L dt \end{align*}$

په لاندې فورمول کې، د عددي محاسبې حدود د تېرو تاريخ او يا د لومړني شرائطو په اساس ټاکل شوي دي، يعني له $-\infty \,\, to \,\, t(0^-)$ .

اوس، را تصور کوو چې د بدلون اقدام په t=0 وخت کې ترسره کيږي، يعني د سويچ بندول په t=0 وخت کې ترسره کيږي. موږ د انډوکټر له لارې د جريان معادله لرو، لکه:

$\begin{align*} i_L = \frac{1}{L} \int v_L dt \end{align*}$

د انتګرال لیموونه دوه وقفې ته جلا کولی شئ $-\infty \,\, to \,\, 0$ او $0 \,\, to \,\,t$ . معلومه چې $0^-$ د سویچ کولو لپاره په لاندې وخت کې ده، په هرصورت چې $0^+$ د سویچ کولو لپاره په بالای وخت کې ده. پس له دا لنډه کولو سره، ما داسې نوي کولی شئ

$\begin{align*} i_L = \frac{1}{L} \int_{-\infty}^{t} v_L dt \end{align*}$

پس،

$\begin{align*} i_L = \frac{1}{L} \int_{-\infty}^{0^-} v_L dt + \frac{1}{L} \int_{0^-}^{t} v_L dt \end{align*}$

دا موده کې، د $\frac{1}{L} \int_{-\infty}^{0^-} v_L dt$ شمېر د ګټې جاري د تاریخی پریود کې د قیمت راښکونه او دا هېڅ نه دی چې د $i_L$ د اولیو شرایط. دا د $i_L(0^-)$ لپاره د اشاره کولو لپاره استعمال کړئ.

$\begin{align*} i_L = i_L(0^-) + \frac{1}{L} \int_{0^-}^{t} v_L dt \end{align*}$

د $t=0^+$ لپاره، ما داسې لیکلی کوو:

$\begin{align*} i_L (0^+)= i_L(0^-) + \frac{1}{L} \int_{0^-}^{0^+} v_L dt \end{align*}$

دا ورته، مونه چې د تبادلې عملیات یې د صفر زمانه کې ترسره کیږي. په دا توګه، انتگرال لرونکي $0^-$ تر $0^+$ څخه د ځای ده.

پس،

$\begin{align*} i_L(0^-) = i_L(0^+) \end{align*}$

پس، د انډوکټر څخه د جریان نشي به سریعه بدلون کوي. دا یعنی د انډوکټر څخه د جریان، د تبادلې عملیات له په اوږد شوی او پسې یو شوی دی.

انډوکټر په t=0 کې

د انډوکټر لپاره $t = 0$ ، یعنی د انډوکټر ته د ولټاژ وړاندې کولو موده، دا د ایدئالو لپاره $\infty$ دی چې د وخت پراخه $dt$ صفر دی. په دې توګه د وخت ته د انډوکټر یو اوپن سرکټ څخه عمل کوي. په استویي حالت کې د $t = \infty$ وخت کې دا د شورت سرکټ څخه عمل کوي.

که د انډوکټر په لاندې وخت کې د اولیو جريانونه I۰ راوړي، نو په $t=0^+$ وخت کې دا د ثابت جرياني سورس څخه عمل کوي او د قيمت $I_0$ دی، په استویي حالت کې د $t=\infty$ وخت کې دا د شورت سرکټ څخه عمل کوي په يو جرياني سورس کې.

سری او پارالل انډوکټران

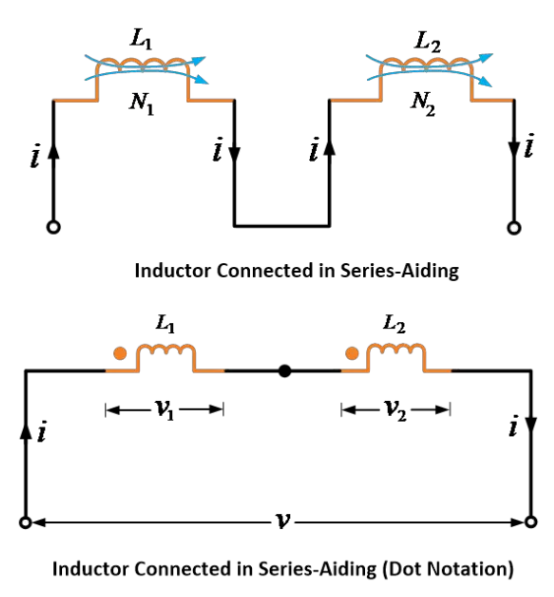
د سریال او پراولو لپاره د ریزیستانو په مانند د انډکټرانو خوندونه کېږي. دوه مغناطیسی توپیر لرونکي کویلونه ۱ او ۲ غواړئ چې خپل-انډکتانس $L_1$ او $L_2$ دا د هنری وحدې له لارې د دوه کویلونو ترمنځ د متبادل انډکتانس.

د الکترونیکی سریال کې دوه انډکټران مختلف څېړنې سره جوړ شوي کېږي چې د داسې د معادل انډکتانس څو مختلف ارزښتونه ده چې په پایلو کې خبرې شوي دي.

سریال انډکټرانو فرمول

سریال انډکټرانو څوګړل

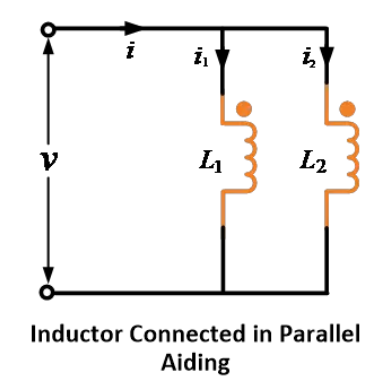
د دوه مغناطیسی توپیر لرونکو انډکټرانو یا کویلونو په سریال کې جوړولو ته د نظر بېرته ورکړئ. د انډکټرانو په سریال کې جوړولو دوه احتمالي څېړنې شتون لري.

د یوه څېړنې کې، د انډکټرانو لخوا تولید شوي فلکسونه د یو بل سمت کې کاري کوي. پس دا انډکټران د سریال-اعمالي یا جمعي څېړنې ته په نوم یادیږي.
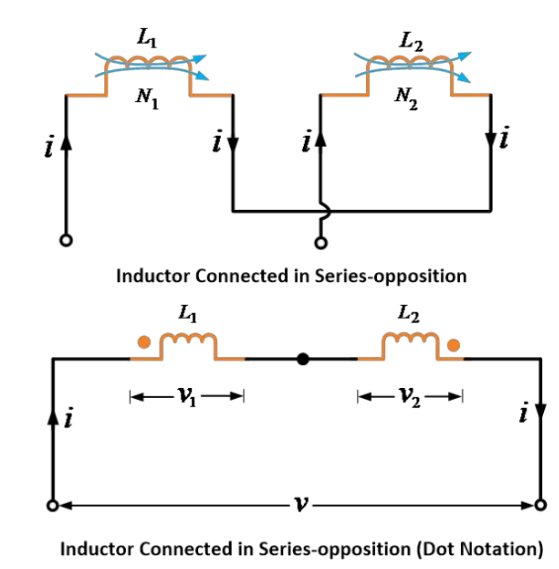
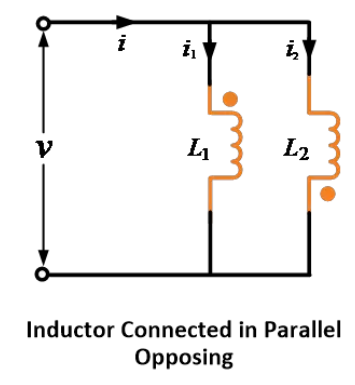
د دویمه څېړنې کې، که د نورو انډکټر لپاره کورنۍ واخلي او دا د فلکسونو ترمنځ د وړاندې کاري کوي، پس دا انډکټران د سریال-مخالفت یا تفریقي څېړنې ته په نوم یادیږي.

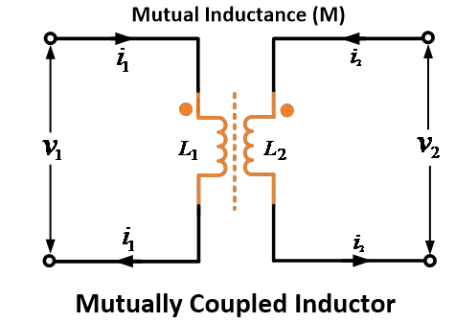
د اینډکټر ۱ خودکار لیپسې $L_1$ او د اینډکټر ۲ خودکار لیپسې $L_2$ . دوی اینډکټرونه څخه د متحاکمې لیپسې M سره متحاکمه شوي.

سریالی ترمنځ (کامولو) تړل (متحاکمې طورتوب جوړښت د خودکار طورتوب جوړښتونه کې یې کمک ورکوي)

دوی اینډکټرونه یا کویلونه د سریالی ترمنځ یا کامولو ډول سره تړل شوي دي، په لاندې تصویر کې ښیي.

دا ترمنځ کې د دوی اینډکټرونو خودکار او متحاکمې فلوکسونه د یو ډول د ځای کې عمل کوي؛ پس د خودکار او متحاکمې طورتوب جوړښتونه هم د یو ډول د ځای کې وي.

پس،

د اینډکټر ۱ خودکار طورتوب جوړښت, $e_s_1 = -L_1\frac{di}{dt}$
د اینډکټر ۱ متحاکمې طورتوب جوړښت, $e_m_1 = -M\frac{di}{dt}$
د اینډکټر ۲ خودکار طورتوب جوړښت, $e_s_2 = -L_2\frac{di}{dt}$
د لانډې ۱ کې متقابل القاء شوي e.m.f، $e_m_2 = -M\frac{di}{dt}$

د ترکیب په وچ کې کلی القاء شوي e.m.f،

$\begin{align*} e=-(L_1\frac{di}{dt}+M\frac{di}{dt}+L_2\frac{di}{dt}+M\frac{di}{dt}) \end{align*}$

(1) $\begin{equation*} e = -(L_1+L_2+2M) \frac{di}{dt} \end{equation*}$

اگر $L_eq$ دوه لانډو درې د سریالي ټولنې یوازې د معادل القایي ځانګړتوب وي، د ترکیب په وچ کې القاء شوي e.m.f په اساسي توګه داسې ده:

(2) $\begin{equation*} e = -L_e_q_. \frac{di}{dt} \end{equation*}$

معادلات (1) او (2) را واورئ، ما داسې بدليږي:

(۳) $\begin{equation*} L_e_q_. = L_1 + L_2 + 2M \end{equation*}$

دا معادله دوه سیریالی او اضافي وړاندې شوي انډکټرونو یا کویلونو د معادل انډکتانس ترلاسه کوي.

که دوه کویلونو ترمنځ د متبادل انډکتانس نه وي (يعني، M = 0)، په اینده،

$\begin{align*} L_e_q_. = L_1 + L_2 \end{align*}$

سری تضاد (دیفرانسیل) وړاندیز (متبادل القایی EMF د خود القایی EMF ته تضاد کوي)

یو باره که دوه متبادل وړاندې شوي انډکټرونو یا کویلونه د سری ترتیب سره وړاندې شول دي، چې دوی د فلوکسونه ترمنځ د تضاد لري، په لوښی کې ښیي.

چونکه د فلوکسونه ترمنځ د تضاد لري، د متبادل القایي EMF د خود القایي EMF ته تضاد کوي. په اینده،

د یوام کویل د خود القایي EMF، $e_s_1 = -L_1\frac{di}{dt}$
د اینډکټر ۱ کې متقابل القاء شوي ولټیژن، $e_m_1 = +M\frac{di}{dt}$
د اینډکټر ۲ کې خودالقاء شوي ولټیژن، $e_s_2 = -L_2\frac{di}{dt}$
د اینډکټر ۲ کې متقابل القاء شوي ولټیژن، $e_m_2 = +M\frac{di}{dt}$

د ترکیب کې په کلی د القا شوي ولټیژن،

$\begin{align*} e=-(L_1\frac{di}{dt}-M\frac{di}{dt}+L_2\frac{di}{dt}-M\frac{di}{dt}) \end{align*}$

(۴) $\begin{equation*} e = -(L_1+L_2-2M) \frac{di}{dt} \end{equation*}$

که $L_e_q$ دوه اینډکټرونو د سیري زړه کې د معادل انډکتانس وي، د ترکیب کې القا شوي ولټیژن به داسې د لارښوونه څخه ورکول شي،

(5) $\begin{equation*} e = -L_e_q_. \frac{di}{dt} \end{equation*}$

د معلوماتو (4) او (5) په مقایسه کې، ما داسې ترلاسه کړو،

(6) $\begin{equation*} L_e_q_. = L_1 + L_2 - 2 M \end{equation*}$

دا معادله دوه اندوکټرونه چې په سلسله وړاندیز یا دifferential connection لپاره دمعادل inductance ته راوړي.

که دوه کویلونه تر میانه دmutual inductance نه وي (يعني M = 0)، نو،

$\begin{align*} L_e_q_. = L_1 + L_2 \end{align*}$

مثال 1

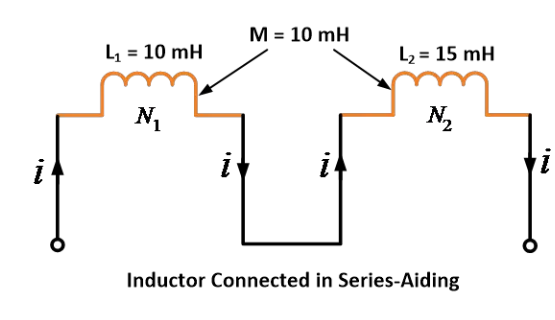
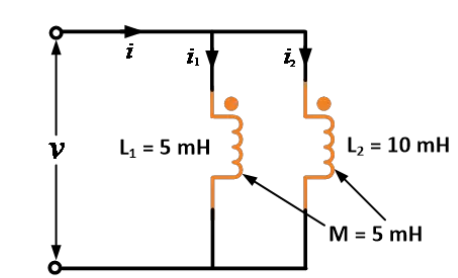
دوه کویلونه د self-inductances 10 mH او 15 mH او دmutual inductance میاشتوبه 10 mH دی. د serie aiding لپاره دمعادل inductance ته په توګه په څرګنده کړئ.

حل:

د دې د معلوماتو د لاندې: L1 = 10 mH، L2 = 15 mH او M = 10 mH

د سلسله کې د ترمنځ پرتله فرمول له منظر:

$\begin{align*} \begin{split} & L_e_q_. = L_1 + L_2 + 2M \\ & = 10 + 15 + 2(10) \\ & = 10 + 15 + 20 \\ & L_e_q_. = 45\,\,mH \end{split} \end{align*}$

په دې فرمول کې د استعمالو توګه، د سلسله کې د ترمنځ پرتله وخت د 45 mH د همپاکې لازمیت اخلي.

مثال ۲

دوه کویلونه د خپلې لازمیتونه 10 mH او 15 mH او د دوه کویلونو ترمنځ د همپاکې لازمیت 10 mH دی. د سلسله کې د ترمنځ پرتله وخت د همپاکې لازمیت جوړ کړئ.

حل:

د دې د معلوماتو د لاندې: L1 = 10 mH، L2 = 15 mH او M = 10 mH

د سلسله کې د ترمنځ پرتله فرمول له منظر:

$\begin{align*} \begin{split} & L_e_q_. = L_1 + L_2 - 2M \\ & = 10 + 15 - 2(10) \\ & = 10 + 15 - 20 \\ & = 25 - 20 \\ & L_e_q_. = 5\,\,mH \end{split} \end{align*}$

دا په معادله کې د څخه، د سریالو تړلو لپاره د مساواتو له طرف سره د هم وړاندې د ۵ ملی هنری د ټولو مساواتو لرونکي د ښودل شوي.

د تړلونو په موازی توګه فرمول

څو تړلونه په موازی توګه کومې کېږي

دوه تړلونه په موازی توګه کومې کېږي چې

د متقابل د ام.اف.ام. د خپلواکي د ام.اف.ام.ونو د په موازی توګه د یوه د ځانګړي کمک کوي
د متقابل د ام.اف.ام. د خپلواکي د ام.اف.ام.ونو په موازی توګه د یوه د ځانګړي دمخکې کوي

د موازی کمک کوونکي (تجمعی) تړل (د متقابل د ام.اف.ام. د خپلواکي د ام.اف.ام.ونو د په موازی توګه د یوه د ځانګړي کمک کوي)

که دوه تړلونه په موازی توګه کومې شي، د متقابل د ام.اف.ام. د خپلواکي د ام.اف.ام.ونو د په موازی توګه د یوه د ځانګړي کمک کوي، چې په زیرنو شکل کې نښې شوي ده.

د L1 او L2 تړلونو په څخه د جريانونو i1 او i2 او I د ټولو جرياني.

پس،

(7) $\begin{equation*} i = i_1 + i_2 \end{equation*}$

په نتیجه کې،

(8) $\begin{equation*} \frac{di}{dt} = \frac{di_1}{dt} + \frac{di_2}{dt} \end{equation*}$

هر دوه اندوکټرونه کې دوه EMFs پیدا کیږي. یو د خود اندوکسیون له لارې او بل د متقابل اندوکسیون له لارې.

څنګه چې اندوکټرونه په متوازی توګه وړاندې شوي دي، EMFs مساوي دي.

په نتیجه کې،

(9) $\begin{equation*} L_1 \frac{di_1}{dt} + M \frac{di_2}{dt} = L_2 \frac{di_2}{dt} + M \frac{di_1}{dt} \end{equation*}$

$\begin{align*} L_1 \frac{di_1}{dt} - M \frac{di_1}{dt} = L_2 \frac{di_2}{dt} - M \frac{di_2}{dt} \end{align*}$

$\begin{align*} \frac{di_1}{dt} (L_1 - M) = \frac{di_2}{dt} (L_2 - M) \end{align*}$

(10) $\begin{equation*} \frac{di_1}{dt} = (\frac{L_2 - M}{L_1 - M}) \frac{di_2}{dt} \end{equation*}$

په دې توګه، د نومبر (۹) کولو سره د نومبر (۸) ته ورکړئ، دا جوړ شوی:

$\begin{align*} \frac{di}{dt} = (\frac{L_2 - M}{L_1 - M}) \frac{di_2}{dt} + \frac{di_2}{dt} \end{align*}$

(۱۱) $\begin{equation*} \frac{di}{dt} = (1 + \frac{L_2 - M}{L_1 - M}) + \frac{di_2}{dt} \end{equation*}$

که $L_e_q.$ د پارالل وړاندې کویلانونو لخوا د همپوره اندوختنې دا داسې ده، د هغه ته د ایم اف موجوب شوي خواهد

(۱۲) $\begin{equation*} e = L_e_q_. \frac{di}{dt} \end{equation*}$

دا د یو کویل کې د ایم اف موجوب شوی سره برابر دی، یعنی،

$\begin{align*} L_e_q_. \frac{di}{dt} = L_1 \frac{di_1}{dt} + M \frac{di_2}{dt} \end{align*}$

(13) $\begin{equation*} \frac{di}{dt} = \frac{1}{L_e_q_.} [L_1 \frac{di_1}{dt} + M \frac{di_2}{dt}] \end{equation*}$

د $\frac{di_1}{dt}$ د قیمت څخه د (10) معادله ته د (13) معادله ته وړاندې کولو سره، ما په اینځای کې داسې لري:

$\begin{align*} \frac{di}{dt} = \frac{1}{L_e_q_.} [L_1 (\frac{L_2 - M}{L_1 - M}) \frac{di_2}{dt} + M \frac{di_2}{dt}] \end{align*}$

(14) $\begin{equation*} \frac{di}{dt} = \frac{1}{L_e_q_.} [L_1 (\frac{L_2 - M}{L_1 - M}) + M] \frac{di_2}{dt} \end{equation*}$

اوس، د (11) معادله او د (14) معادله یو بل ته ورکول:

$\begin{align*} 1+(\frac{L_2 - M}{L_1 - M}) \frac{di_2}{dt} = \frac{1}{L_e_q_.}[L_1 (\frac{L_2 - M}{L_1 - M}) + M]\frac{di_2}{dt} \end{align*}$

$\begin{align*} \frac{L_1+L_2 - 2M}{L_1 - M} = \frac{1}{L_e_q_.} [\frac{L_1L_2- L_1M+L_1M - M^2}{L_1 - M}] \end{align*}$

$\begin{align*} \frac{L_1+L_2 - 2M}{L_1 - M} = \frac{1}{L_e_q_.} [\frac{L_1L_2 - M^2}{L_1 - M}] \end{align*}$

(15) $\begin{equation*} L_e_q_. = \frac{L_1L_2 - M^2}{L_1+L_2 - 2M} \end{equation*}$

دا معادله دوه سپرې کویلونه چې په موازۍ توګه او ترسره کړي د ورته درنډونه لپاره د معادل درنډونه راوباسئ.

که دوه کویلونو ترمنځ د همکاري درنډ نه وي (يعني، M = 0)، په اینده:

$\begin{align*} L_e_q_. = \frac{L_1L_2 - (0)^2}{L_1+L_2-2(0)} = \frac{L_1L_2}{L_1+L_2} = \frac{product}{sum} \end{align*}$

پارالېل مخالفت (دیفرانسیل) اړیکه (متعادل شوي متقابل القاء د خود القاء مخالفت)

دو ګټونو په پارالېل مخالفت کې وصل شولو کې، متعادل شوي متقابل القاء د خود القاء مخالفت کوي.

اوږدۍ داسې ښودل شوې دوه ګټونه په پارالېل مخالفت یا دیفرانسیل ډول وصل شوي دي.

د پارالېل سرچینې اړیکې ډول به داسې ثابت کړي چې،

(۱۶) $\begin{equation*} L_e_q_. = \frac{L_1L_2 - M^2}{L_1+L_2 + 2M} \end{equation*}$

دا معادله دوه ګټونو په پارالېل مخالفت یا دیفرانسیل ډول وصل شوو ګټونو د معادل ګټنې ترلاسه کوي.

که دوه ګټونو ترمنځ د متقابل القاء نه وي (يعني M = 0)، نو،

$\begin{align*} L_e_q_. = \frac{L_1L_2 - (0)^2}{L_1+L_2+2(0)} = \frac{L_1L_2}{L_1+L_2} = \frac{product}{sum} \end{align*}$

نمونه ۱

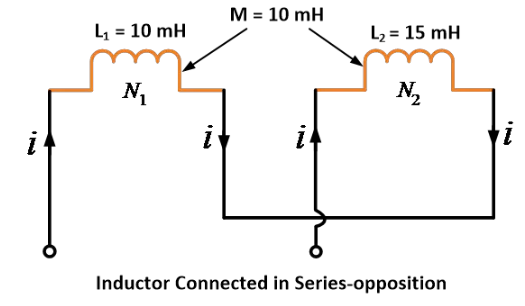
دو سپریت که د اودلوالۍ خود سپریت ۵ میلی هنری او ۱۰ میلی هنری دي او دویمی سپریت ۵ میلی هنری دي. په موازی سره یې د جوړولو لپاره د معادل سپریت یې وړاندیز کړئ.

حل:

د دې داتا: L1 = ۵ میلی هنری، L2 = ۱۰ میلی هنری او M = ۵ میلی هنری

په موازی سره یې د جوړولو فرمول برابری:

$\begin{align*} \begin{split} & L_e_q_. = \frac{L_1 L_2 - M^2}{L_1 + L_2 - 2M}.... if \,\, fluxes \,\, aid \\ & = \frac{5 * 10 - (5)^2}{5 + 10 - 2(5)} \\ & = \frac{50 - 25}{15 - 10} \\ & = \frac{25}{5} \\ & L_e_q_. = 5\,\,mH \end{split} \end{align*}$

په دې معادله کې د معادل سپریت ۵ میلی هنری یې ترلاسه کړئ که دوه دواړه په موازی سره یې جوړ شوي وي.

نمونه ۲

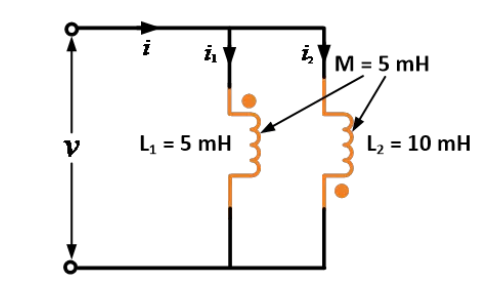
دوه سولېنودونه خپلکړه انډوکټنس ۵ mH او ۱۰ mH لري، او د دواړو ترمنځ مشترک انډوکټنس ۵ mH ده. د موازي ضد اتصال په حالت کې معادل انډوکټنس ومومئ.

حل:

د ورکړل شوی معلومات: L1 = 5 mH, L2 = 10 mH او M = 5 mH

د موازي ضد فورمول له مخی،

$\begin{align*} \begin{split} & L_e_q_. = \frac{L_1 L_2 - M^2}{L_1 + L_2 + 2M}.... if \,\, fluxes \,\, oppose \\ & = \frac{5 * 10 - (5)^2}{5 + 10 + 2(5)} \\ & = \frac{50 - 25}{15 + 10} \\ & = \frac{25}{25} \\ & L_e_q_. = 1\,\,mH \end{split} \end{align*}$

نو د معادلې کارولو سره، کله چې دواړه سولېنودونه موازي ضد نښل شوي وي، معادل انډوکټنس 1 mH ترلاسه کوو.

تړل شوي سولېنودونه

کله چې د يو سولېنود (کوڅکي) مغناطيسي ساحه د بلې وروستۍ سولېنود د ګردېدو کتلې يا تړاو ته ورسېږي، نو دواړه سولېنودونه د مغناطيس تړلي ورته ويل کېږي. د سولېنودونو يا کوڅکو تړلو له امله، د دواړو کوڅکو ترمنځ يو مشترک انډوکټنس شتون لري.

د تړلو سرکيټونو کې، د انرژي انتقال د يو سرکيټ څخه ته بل سرکيټ ته صورت نيسي کله چې يو سرکيټ برق ورکړل شي. دوه څنډې والٹراينس فارمر، يو اتو ټرانسفارمر، او يو انډکشن موټر د مغناطيسي تړل شوي سولېنودونو، يا کوڅکو، يا سرکيټونو د بېلګو څخه دي.

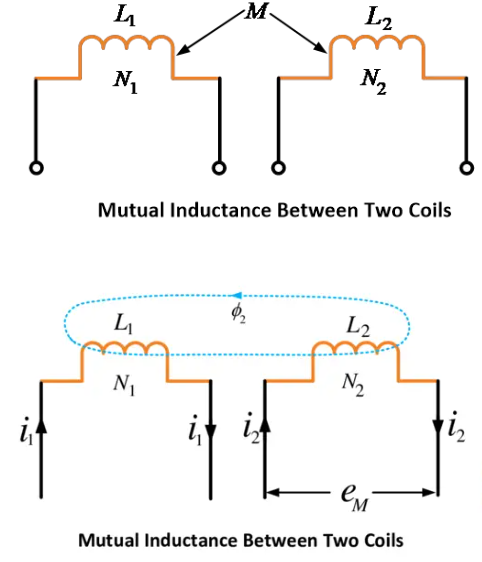
دوه مغناطیسی وړاندې شوي اینډکټرانو یا کویلونه ۱ او ۲ را خپلواک لازم بندیدونکي L۱ او L۲ په توګه ترتیب شوي. M د دوی کویلونو ترمنځ د متقابل بندیدونکو عدد.

د متقابل بندیدونکو اثر یا زیاتول (L۱ + M او L۲ + M) یا کم کول (L۱ – M او L۲ – M) د دوی کویلونو بندیدونکو، دا د دوی کویلونو یا اینډکټرانو جوړښت په بڼه دی.

که دوی کویلونو په چاپیریتوب سره جوړ شوي وي چې د دوی فلوکسونه یو بل یو هم یاری کوي، نو د هر کویل بندیدونکو ترڅو M یعنی L۱ + M د کویل ۱ او L۲ + M د کویل ۲. دا د داسې له امله دی چې د هر کویل ترلاسه کیدو فلوکس د خپل فلوکس څخه زیات دی.
که دوی کویلونو په چاپیریتوب سره جوړ شوي وي چې د دوی فلوکسونه یو بل یو مخالفت کوي، نو د هر کویل بندیدونکو ترڅو M یعنی L۱ – M د کویل ۱ او L۲ – M د کویل ۲. دا د داسې له امله دی چې د هر کویل ترلاسه کیدو فلوکس د خپل فلوکس څخه کم دی.

د متقابل بندیدونکو فرمول

ما د یو کویل کې د جرياني ټولو تبدیلاتو ترڅو د دویمه کویل کې متقابل القاعدي e.m.f. پروژکشن ښودل کېږي.

د متقابل بندیدونکو تعريف د یو کویل (یا د سرچینې) د دویمه کویل (یا د سرچینې) کې e.m.f. پروژکشن کول دی چې د یو کویل کې د جرياني تبدیل ښودل کېږي.

نور یو چیز د یو کویل د خصوصیت دی چې د دویمه کویل کې د جرياني تبدیل په مخالفت کې یې د متقابل بندیدونکو ښودل کېږي. دا د دویمه کویل کې د متقابل القاعدي e.m.f. پروژکشن له امله دی چې د یو کویل کې د جرياني تبدیل په مخالفت کې ښودل کېږي.

د متقابل بندیدونکو (M) تعريف د یو کویل کې د فلوکس لینکج په یو واحد جريان کې د دویمه کویل کې د فلوکس لینکج عدد دی.

د ریاضیو لاره،

$\begin{align*} M = \frac{N_2 \phi_1_2}{I_1} \end{align*}$

که،

$I_1$ = په اولو کویل کې جریان

$\phi_1_2$ = دوه ام تور کویل ته وړاندیز شوي فلوکس

$N_2$ = دوه ام تور کویل ته وړاندیز شوي لوپونه

دوه کویلونو ترمنځ د متقابل القائیت ۱ هنری دی چې یو کویل ته په یو آمپیر له نرخ څخه جریان بدلون کېږي او د بیا کویل ته یو ولټ ولټ ایم اف القایيږي.

د وړاندېزې ضریب

د دوه کویلونو ترمنځ د وړاندېزې ضریب (k) د یو کویل ته وړاندیز شوي جریان لرونکي مغناطیسي فلوکس د بیا کویل ته وړاندیز شوي فراوانۍ ډله دی.

کوپل شوي مدارونه کې د کوپل شوي کویلونو ترمنځ د کوپل شوې مقدار تعيين کول لپاره د کوپلینګ د ضريب مهمه پارامتر دی.

رياضياتي توګه، د کوپلینګ د ضريب جوړښت کېدای شي،

$\begin{align*} k = \frac{M}{\sqrt{L_1L_2}} \end{align*}$

که:

L1 د نومبر يوه کویل د خپلواکي اندازه دی

L2 د دويمه کویل د خپلواکي اندازه دی

M د دوه کویلونو ترمنځ د مشترکو اندازه دی

د کوپلینګ د ضريب د دوه کویلونو ترمنځ د مشترکو اندازه په اساس ښودل کیږي. که د کوپلینګ د ضريب لوی وي، نو د مشترکو اندازه هم لوی وي. دوه کوپل شوي کویلونه د مغناطيسي فلوکس له لارې پیوند شوي دي.

که يوه کویل د بل کویل سره د تمام فلوکس پیوند شوي وي، نو د کوپلینګ د ضريب ۱ (يعني ۱۰۰٪) وي، او کویلونه چې د وړاندې کوپل شوي دي.
که يوه کویل د بل کویل سره د نیمه فلوکس پیوند شوي وي، نو د کوپلینګ د ضريب ۰.۵ (يعني ۵۰٪) وي، او کویلونه چې د واچنې کوپل شوي دي.
که يوه کویل د بل کویل سره د فلوکس په لاسه پیوند نه وي، نو د کوپلینګ د ضريب ۰ وي، او کویلونه چې د مغناطيسي لارې جلا شوي دي.

د کوپلینګ د ضريب همیشه یوڅخه ډیر نه وي. دا د کرنۍ موادونو په اساس ښودل کیږي. د هوایي کرنۍ لپاره، د کوپلینګ د ضريب ۰.۴ تر ۰.۸ پورې وي چې د دوه کویلونو ترمنځ د فاصلې په بڼه دی او د آهن يا فریټ کرنۍ لپاره دا ۰.۹۹ تر ډېر وي.

سرچینه: Electrical4u.

د اصلي لپاره احترام، خوښه مقالې جوړولو لپاره، که ناروغۍ شته مخې پاتې کړئ.