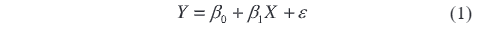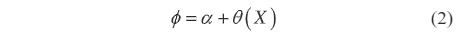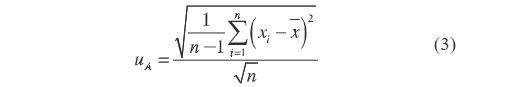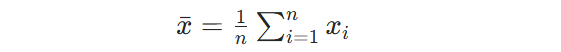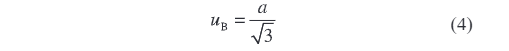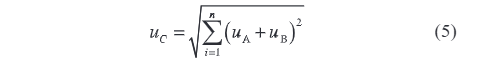Procjena neizvjesnosti mjerenja mrežnog elektroničkog transformatora napona

1. Uvod

Mrežni elektronički naponski transformatori, kao neizostavni mjerilni komponenti u elektroenergetskim sustavima, imaju svoju točnost mjerenja direktno vezanu za stabilno funkcioniranje i učinkovito upravljanje elektroenergetskim sustavima. Međutim, u praksi, zbog inherentnih karakteristika elektroničkih komponenti, okruženjskih faktora i ograničenja metoda mjerenja, rezultati mjerenja naponskih transformatora često uključuju neizvjesnosti. Ova neizvjesnost ne samo da utječe na točnost podataka o snazi, već i zavodi strategije raspoređivanja, kontrole i zaštite elektroenergetskih sustava. Stoga je duboko istraživanje metoda procjene neizvjesnosti za provjeru i rezultate mjerenja mrežnih elektroničkih naponskih transformatora ključno za poboljšanje točnosti mjerenja u elektroenergetskim sustavima.

Ovo istraživanje ima za cilj sistematsku analizu faktora koji utječu na neizvjesnost mjerenja naponskih transformatora, uključujući temperaturni drift, starenje i šumski smetnje elektroničkih komponenti, kao i promjene temperature, vlažnosti i elektromagnetskih polja u okruženju mjerenja. Kroz to će se istraživati znanstvene i razumne metode procjene neizvjesnosti. Stvaranjem matematičkih modela kombiniranih s statističkim principima i znanjem o metrologiji, ovo istraživanje će kompjelativno procijeniti neizvjesnost mjerenja mrežnih elektroničkih naponskih transformatora u različitim radnim uvjetima, pružajući teorijsku osnovu i tehničku podršku za izradu preciznijih propisa za provjeru i poboljšanje kvalitete proizvoda naponskih transformatora.

2. Eksperiment za procjenu neizvjesnosti rezultata mjerenja
2.1 Eksperimentalni objekt

Za procjenu neizvjesnosti mrežnih elektroničkih naponskih transformatora odabran je precizni kalibracijski uređaj za napon s točnošću razine 0,001, koji pokriva opseg mjerenja od 1–1000 V. Naponski transformator koji se provjerava dizajniran je za scenarije s primarnim naponom od 10 kV–50 kV i sekundarnim naponom od 100 V, s razinom točnosti 0,02. Struktura mrežnog elektroničkog naponskog transformatora prikazana je na slici 1.

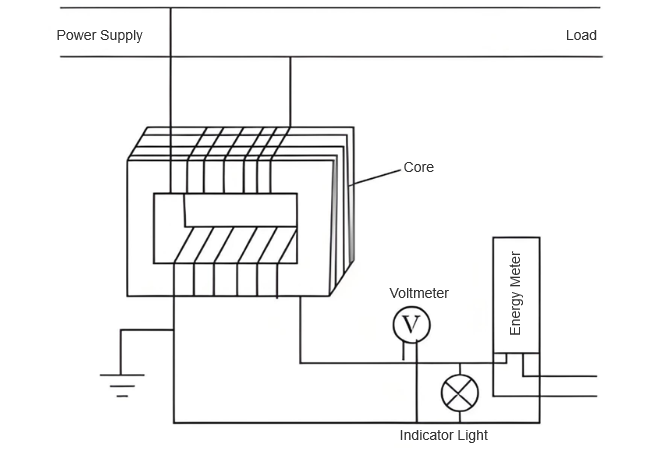
Eksperimentalno okruženje postavljeno je na konstantnu temperaturu od 20 ± 2 °C, s relativnom vlažnošću održavanom ispod 60%, eliminirajući potencijalni utjecaj okruženja na rezultate mjerenja.

2.2 Metoda provjere i mjerenja mrežnih elektroničkih naponskih transformatora

Tijekom provjere mrežnih elektroničkih naponskih transformatora, potrebna je znanstvena metoda procjene neizvjesnosti kako bi se osigurala točnost mjerenja. Koristeći mrežni elektronički naponski transformator prikazan na slici 1 kao standardni uređaj, koristi se usporedna veza kruga. To omogućuje bezprekidnu poravnanje između testiranog elektroničkog naponskog transformatora i standardnog uređaja, kao što je prikazano na slici 2.

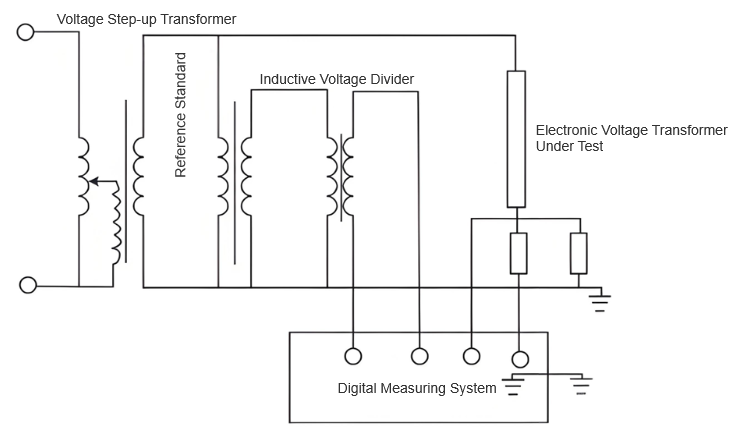
Nakon toga, visokotočan digitalni mjerne sustav direktno čita i izračunava grešku testiranog elektroničkog naponskog transformatora. Model standardnog uređaja je DHBV-110/0.02, s odličnom točnošću koja podupire provjeru. Za testiranu transformatoru, postavljena su nominalne točke napona od 0,5 %, 2 %, 10 %, 50 % i 110 % kako bi se pokrilo njeno radno područje. Važno je napomenuti da iako su maksimalni dopušteni limesi grešaka za ove točke isti u slučaju punog i lakšeg opterećenja, temperaturni drift i starenje elektroničkih komponenti mogu uzrokovati značajne razlike u stabilnosti u različitim uvjetima. Stoga mora se nezavisno procijeniti stabilnost svake točke kako bi se kontrolirala neizvjesnost rezultata provjere, zadovoljavajući stroge zahtjeve za visokotočnim mjerilnim tehnologijama u operaciji elektroenergetske mreže.

3. Matematički model

U eksperimentu za procjenu neizvjesnosti rezultata provjere i mjerenja mrežnih elektroničkih naponskih transformatora, tijekom provjere točnosti testiranog uređaja, njegova neizvjesnost često se kvantificira preko više dimenzija, poput odstupanja točnosti i faza lag. Ovi dva pokazatelja odražavaju amplitudnu razliku i faznu deviaciju između izmjerene vrijednosti i stvarne vrijednosti, redom. Stoga se mogu izgraditi nezavisni matematički modeli kako bi se točno opisali ovi izvori neizvjesnosti. Za odstupanje točnosti Y može se koristiti linearni regresijski model, izražen kao:

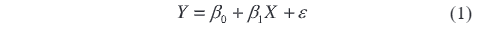
Gdje su β0 i β1 parametri modela; X je ulazni signal mrežnog elektroničkog naponskog transformatora; ε je slučajna greška. Za fazni lag φ može se izraziti trigonometrijskim funkcionalnim modelom kao

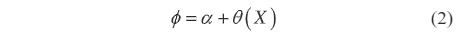
Gdje α predstavlja fiksni fazni pomak; θ(X) je fazna funkcija koja varira s ulaznim signalom. Za detaljniju analizu, mogu se uvesti nelinearni pojmovi ili polinomijalne aproksimacije kako bi se povećala točnost modela. Stvaranje ovih matematičkih modela pruža čvrstu teorijsku osnovu i kvantitativne alate za kompjelativnu i sistematiziranu procjenu neizvjesnosti rezultata mjerenja.

4. Rezultati eksperimenta procjene komponente neizvjesnosti

U provjeri mrežnih elektroničkih naponskih transformatora, postavljene su više skupina nivoa napona za procjenu neizvjesnosti. Odabrane su nominalne točke napona od 0,5 %, 2 %, 10 %, 50 % i 110 % i izmjerene su usporednim metodom. Prosječne vrijednosti amplitudne razlike i fazne deviacije su zabilježene i izračunate kao referentne vrijednosti na odgovarajućim nivoima napona kako bi se točno procijenila neizvjesnost performansi testiranog transformatora.

4.1 Procjena tipa A neizvjesnosti

Tip A neizvjesnosti odražava stupanj disperzije među rezultatima dobivenim tijekom ponovljenih mjerenja istog objekta. Njegov izračunavanje je:

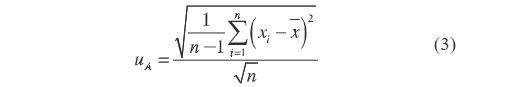
Gdje n je broj mjerenja; xi je i-ti izmjerena vrijednost; x̄ je aritmetička sredina izmjerene vrijednosti.

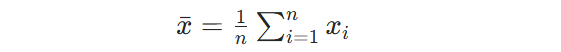
Zatim, za nominalne točke napona od 0,5 %, 2 %, 10 %, 50 % i 110 %, rezultati procjene tipa A neizvjesnosti prikazani su u tablici 1.

Kao što se može vidjeti iz tablice 1, s porastom nominalne točke napona, tip A neizvjesnosti za amplitudnu razliku i faznu deviaciju pokazuje tendenciju rasta. To je zato što na nižim nivoima napona, naponski transformator je stabilniji, što rezultira manjom disperzijom u rezultatima mjerenja. Međutim, na višim nivoima napona, naponski transformator je pod utjecajem više faktora, što dovodi do veće disperzije u rezultatima mjerenja.

4.2 Procjena tipa B neizvjesnosti

Prema JJF 1059.1—2022 Procjena i izraz neizvjesnosti mjerenja, tip B neizvjesnost dolazi od razumne inferencije poznatih relevantnih informacija kako bi se procijenila njegova standardna devijacija. Ove informacije mogu uključivati specifikacije opreme od proizvođača, podatke o industrijski prepoznatim metodama kalibracije ili statističku analizu povijesnih podataka mjerenja. Srž tipa B neizvjesnosti je definiranje mogućeg intervala varijacije izmjerene vrijednosti temeljem iskustva ili stručnog znanja, s njegovom poluširinom koja je polovina širine intervala.

Zatim, odaberite odgovarajući faktor pokrivanja k za kvantifikaciju prema karakteristikama vjerojatnosne distribucije i potrebnom stupnju pouzdanosti. Obično, ako su izmjerene vrijednosti uniformno distribuirane unutar predodređenog intervala (svaka vrijednost ima jednak vjerojatnost), koristi se model uniformne distribucije, a k može se uzeti kao aproksimacija √3 kako bi se osigurala točnost i rigoroznost procjene. Izračunavanje tipa B neizvjesnosti je

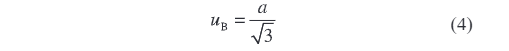
Gdje a je poluširina intervala varijacije mjerenja.

Za nominalne točke napona od 0,5 %, 2 %, 10 %, 50 % i 110 %, rezultati procjene tipa B neizvjesnosti prikazani su u tablici 2.

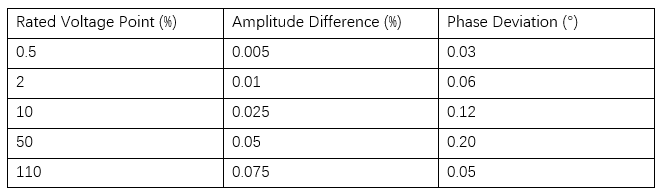
Kao što se može vidjeti iz tablice 2, na različitim nominalnim točkama napona, bilo za amplitudnu razliku ili faznu deviaciju, neizvjesnost pokazuje tendenciju rasta s porastom nivoa napona. U usporedbi s tipom A neizvjesnosti, procjena tipa B neizvjesnosti više se oslanja na točnost i kompletnost poznatih informacija, odražavajući priopćeni procjenu performansi mjerene naponske transformatora. Stoga, u praktičnim primjenama, kompjelativno razmatranje tipa A i tipa B neizvjesnosti omogućuje potpuniju kontrolu nad točnošću i pouzdanosti rezultata mjerenja.

4.3 Procjena kombinirane standardne neizvjesnosti

Tijekom procjene kombinirane standardne neizvjesnosti, ako su rezultati provjere i mjerenja svakog mrežnog elektroničkog naponskog transformatora nezavisni i nekorelirani (to jest, njihovi koeficijenti korelacije su svi 0), neizvjesnosti slijede princip linearne kombinacije za akumulaciju. Na temelju toga, procjena kombinirane standardne neizvjesnosti može se izraziti sljedećom formulom

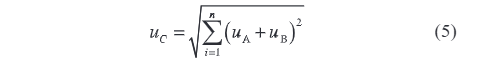
Zatim, za nominalne točke napona od 0,5 %, 2 %, 10 %, 50 % i 110 %, rezultati procjene kombinirane standardne neizvjesnosti prikazani su na slici 3.

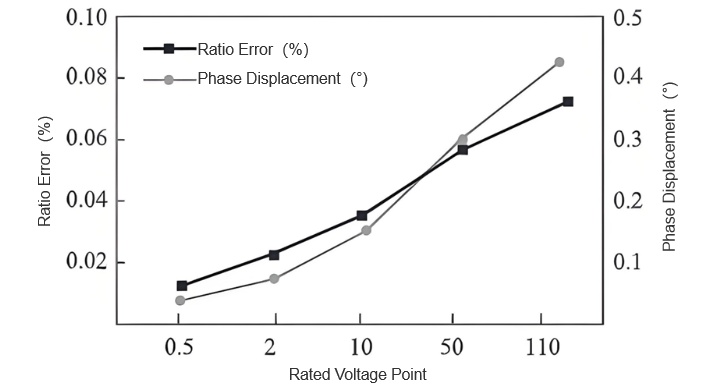
Iz rezultata slike 3, s porastom nominalnog napona od 0,5 % do 110 %, kombinirane standardne neizvjesnosti za amplitudnu razliku i faznu deviaciju pokazuju stabilni rast. Konkretno, neizvjesnost amplitudne razlike poraste s 0,008 % na 0,085 % (oko deset puta), a neizvjesnost fazne deviacije poraste s 0,05° na 0,35° (oko sedam puta). Ova tendencija sugerira da viši napon povećava osjetljivost transformatora na vanjske smetnje, proširujući neizvjesnost mjerenja. Ipak, ne događaju se ekstremne promjene podataka, što ukazuje na stabilnost i pouzdanost procesa procjene.

5. Zaključak

U istraživanju metoda procjene neizvjesnosti rezultata provjere i mjerenja mrežnih elektroničkih naponskih transformatora, analizirani su mnogi faktori koji utječu na točnost mjerenja, a istraživani su znanstveni i učinkoviti metodi procjene. Kroz teorijsku analizu i eksperimentalnu verifikaciju, ne samo je poboljšana pouzdanost rezultata mjerenja naponskih transformatora, već je pružena čvrsta jamstva za stabilno funkcioniranje elektroenergetske mreže.