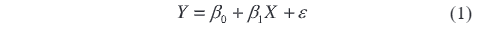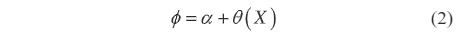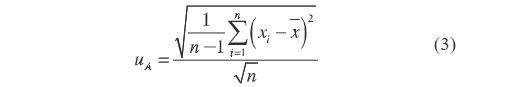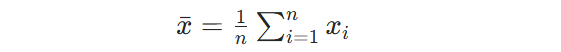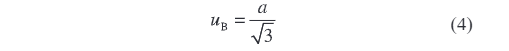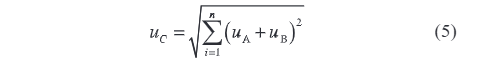Usikkerhedsvurdering for måling af netvoltageoverfører

1. Introduktion

Netvoltageoverførere, som uundværlige måleenheder i kraftsystemer, har deres målnøjagtighed direkte knyttet til den stabile drift og effektive forvaltning af kraftsystemer. I praksis påvirkes måleresultaterne imidlertid ofte af usikkerhed på grund af de elektroniske komponenters indbyggede egenskaber, miljøfaktorer og begrænsninger i målemetoder. Denne usikkerhed påvirker ikke kun nøyagtigheden af strømdata, men kan også mislede kraftsystemets planlægning, kontrol og beskyttelsesstrategier. Derfor er en grundig undersøgelse af usikkerhedsbedømmelsesmetoder for verificering og måling af netvoltageoverførere afgørende for at forbedre målnøjagtigheden i kraftsystemer.

Denne studie sigter mod at systematisk analysere faktorer, der påvirker målusikkerheden af voltageoverførere, herunder temperaturdrift, aldring og støjforstyrrelser af elektroniske komponenter, samt ændringer i temperatur, fugtighed og elektromagnetiske felter i målemiljøet. Gennem dette vil videnskabelige og rimelige usikkerhedsbedømmelsesmetoder blive undersøgt. Ved at opbygge matematiske modeller kombineret med statistiske principper og metrologi-kendskab vil denne undersøgelse gennemgående vurdere målusikkerheden af netvoltageoverførere under forskellige arbejdssituationer, hvilket giver en teoretisk basis og teknisk støtte for at udarbejde mere præcise verifikationsregler og forbedre produktkvaliteten af voltageoverførere.

2. Eksperiment for Vurdering af Målingens Usikkerhed
2.1 Eksperimentelt Objekt

For usikkerhedsbedømmelse af netvoltageoverførere er et præcisionsspændingskalibreringsanlæg med en nøjagtighed på 0,001 niveau valgt, der dækker et målingsområde fra 1–1000 V. Den voltageoverfører, der skal verificeres, er designet til scenarier med en primærspænding på 10 kV–50 kV og en sekundærspænding på 100 V, med et nøjagtighedsniveau på 0,02. Strukturen af netvoltageoverføreren vises i figur 1.

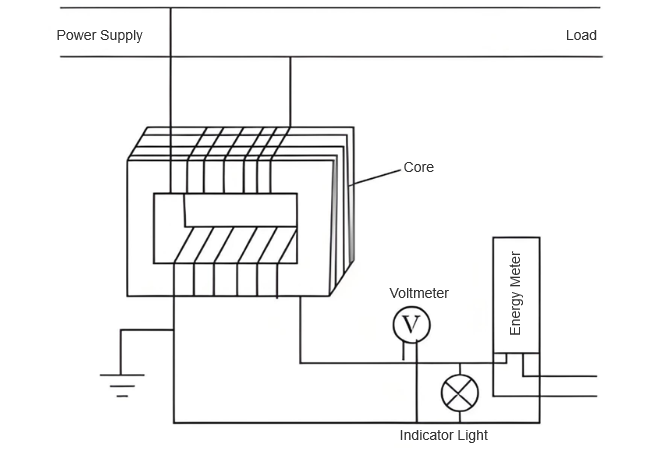
Eksperimentmiljøet er sat til en konstant temperatur på 20 ± 2 °C, med relativ fugtighed holdt under 60%, for at eliminere potentielle miljøpåvirkninger på måleresultater.

2.2 Verifikations- og Målemetode for Netvoltageoverførere

Under verifikationen af netvoltageoverførere er en videnskabelig usikkerhedsbedømmelsesmetode nødvendig for at sikre målenøjagtighed. Ved at bruge netvoltageoverføreren vist i figur 1 som standardenhed, anvendes en sammenligningsbaseret kredsløbsforbindelse. Dette muliggør en seemløs justering mellem den testede elektroniske voltageoverfører og standardenheden, som vist i figur 2.

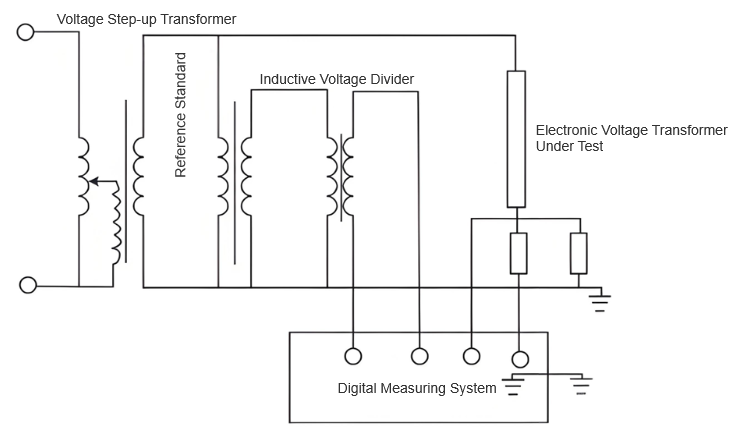
Herefter læses og beregnes fejlen i den testede elektroniske voltageoverfører direkte ved hjælp af et højpræcisionst digitalt målesystem. Standardenhedens model er DHBV-110/0.02, med fremragende nøjagtighed, der understøtter verifikationen. For den testede transformer er nulpunkter for nominel spænding på 0,5 %, 2 %, 10 %, 50 % og 110 % sat for at dække dens driftsområde. Bemærk, at selvom maksimalt tilladt fejlgrænse for disse punkter er det samme under fuld- og letbelastning, kan temperaturdrift og aldring af elektroniske komponenter give betydelige stabilitetsforskelle over forholdene. Derfor skal hver punkts stabilitet evalueres uafhængigt for at kontrollere verifikationsresultatets usikkerhed, og møde kraftnets drifts strenge krav til højnøjagtig måleteknologi.

3. Matematisk Model

I eksperimentet for vurdering af usikkerheden af verifikations- og måleresultater for netvoltageoverførere, når man verificerer enhedens nøjagtighed, kvantificeres ofte usikkerheden gennem flere dimensioner, såsom nøjagtighedsafvigelse og faselag. Disse to indikatorer afspejler henholdsvis amplitudforskellen og fasen afvigelse mellem det målte værdi og den sande værdi. Dermed kan uafhængige matematiske modeller opbygges for at præcist beskrive disse usikkerhedskilder. For nøjagtighedsafvigelsen Y kan en lineær regressionsmodel bruges, udtrykt som:

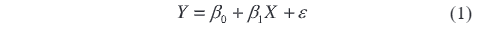
Hvor β₀ og β₁ er modelparametre; X er inputsignal til netvoltageoverføreren; ε er den tilfældige fejlterm. For faselaget φ kan det udtrykkes ved en trigonometrisk funktionsmodel som

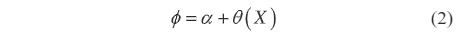
Hvor α repræsenterer den faste faseforskydning; θ(X) er en fasefunktion, der varierer med inputsignalet. For en mere detaljeret analyse kan ikke-lineære termer eller polynomiale tilnærmelser indføres for at forbedre modellens nøjagtighed. Opbygningen af disse matematiske modeller giver en solid teoretisk basis og kvantitative værktøjer for en gennemgående og systematisk vurdering af måleresultaternes usikkerhed.

4. Resultater af Usikkerhedskomponentevalueringsekperimentet

I verifikationen af netvoltageoverførere sættes flere sæt spændingsniveauer for usikkerhedsbedømmelse. Nulpunkterne for nominel spænding på 0,5 %, 2 %, 10 %, 50 % og 110 % er valgt og målt ved hjælp af sammenligningsmetoden. Gennemsnitsværdierne for amplitudforskellen og fasen afvigelse registreres og beregnes som referencetal for de korrespondende spændingsniveauer, for at præcist vurdere den testede transformers ydeevneusikkerhed.

4.1 Type A Usikkerhedsbedømmelse

Type A usikkerhed afspejler graden af spredning blandt resultaterne, der er opnået under gentagne målinger af samme objekt. Beregningsformlen er:

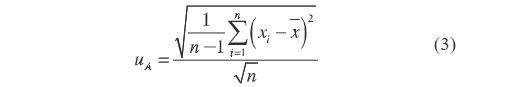
Hvor n er antallet af målinger; x_i er den i-te målte værdi; x̄ er det aritmetiske gennemsnit af de målte værdier.

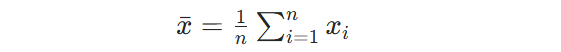
Således, for nulpunkterne for nominel spænding på 0,5 %, 2 %, 10 %, 50 % og 110 %, vises vurderingsresultaterne for Type A usikkerhed i tabel 1.

Som ses i tabel 1, viser både amplitudforskellen og fasen afvigelse en stigende tendens for Type A usikkerhed, mens den nominelle spændingspunkt øges. Dette skyldes, at ved lavere spændingsniveauer er voltageoverføreren mere stabil, hvilket resulterer i mindre spredning i måleresultaterne. Men ved højere spændingsniveauer er voltageoverføreren påvirket af flere faktorer, hvilket fører til større spredning i måleresultaterne.

4.2 Vurdering af Type B Usikkerhed

Ifølge JJF 1059.1—2022 Vurdering og Utryk af Målingens Usikkerhed, kommer Type B usikkerhed fra en fornuftig inferens af kendt relevant information for at estimere dens standardafvigelse. Denne information kan involvere fabrikantens specifikationer, data fra branchen anerkendte kalibreringsmetoder, eller statistisk analyse af historiske målingdata. Kernen i Type B usikkerhed er at definere det mulige variationsområde for den målte værdi baseret på erfaring eller professionel viden, med dets halvdelen af bredde være halvdelen af området.

Derpå vælges en passende dækningsfaktor k for kvantificering ifølge sandsynlighedsfordelingskarakteristikker og ønsket konfidensniveau. Hvis målte værdier er jævnt fordelt inden for det forudbestemte interval (hver værdi har lige stor sandsynlighed), bruges uniform fordelingsmodellen, og k kan tages som en approksimation af √3 for at sikre vurderingsnøjagtighed og strengthed. Beregningsformlen for Type B usikkerhed er

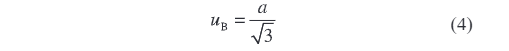
Hvor a er halvdelen af målingens variationsinterval.

For nulpunkterne for nominel spænding på 0,5 %, 2 %, 10 %, 50 % og 110 %, vises vurderingsresultaterne for Type B usikkerhed i tabel 2.

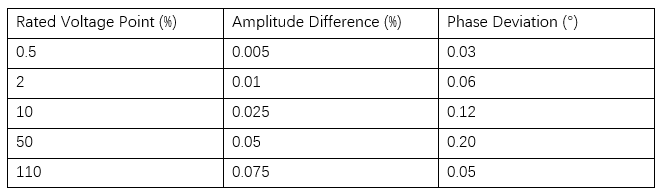
Som ses i tabel 2, viser både amplitudforskellen og fasen afvigelse en stigende tendens for Type B usikkerhed, mens den nominelle spændingspunkt øges. I sammenligning med Type A usikkerhed, afhænger vurderingen af Type B usikkerhed mere af nøjagtigheden og kompletheden af kendt information, hvilket reflekterer en forudgående vurdering af voltageoverførerens ydeevne under måling. Derfor, i praktiske applikationer, giver en omfattende overvejelse af Type A og Type B usikkerheder en mere gennemgående forståelse af måleresultaternes nøjagtighed og pålidelighed.

4.3 Vurdering af Sammensat Standardusikkerhed

Når man vurderer sammensat standardusikkerhed, hvis verifikations- og måleresultater for hver netvoltageoverfører er uafhængige og ukorrelerede (dvs. deres korrelationskoefficienter er alle 0), følger usikkerhederne principet om lineær kombination for akkumulation. Baseret herpå kan vurderingen af sammensat standardusikkerhed udtrykkes ved følgende formel

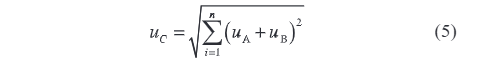
Således, for nulpunkterne for nominel spænding på 0,5 %, 2 %, 10 %, 50 % og 110 %, vises vurderingsresultaterne for sammensat standardusikkerhed i figur 3.

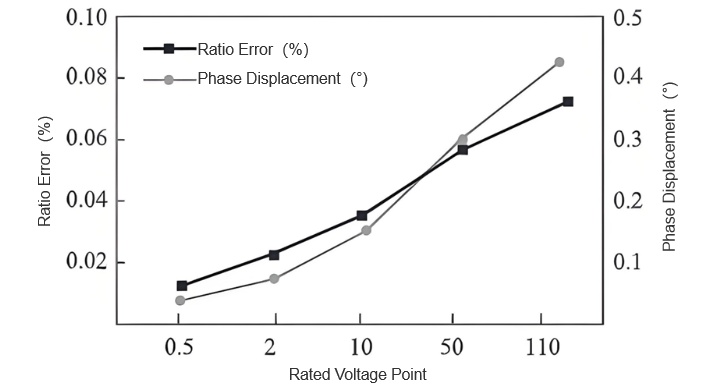
Fra figurs 3 resultater, som den nominelle spænding stiger fra 0,5 % til 110 %, viser sammensatte standardusikkerheder for både amplitudforskellen og fasen afvigelse en stabil stigning. Specifikt, amplitudforskellen usikkerhed stiger fra 0,008 % til 0,085 % (ca. 10-fold), og fasen afvigelse usikkerhed stiger fra 0,05° til 0,35° (ca. 7-fold). Denne tendens implikerer, at højere spænding øger overførerens følsomhed over for eksterne forstyrrelser, hvilket øger målingens usikkerhed. Dog forekommer der ingen ekstreme dataændringer, hvilket indikerer, at vurderingsprocessen er stabil og pålidelig.

5. Konklusion

I undersøgelsen af metoder til vurdering af usikkerhed for verifikation og måling af netvoltageoverførere, analyseres flere faktorer, der påvirker målenøjagtighed, og videnskabelige og effektive bedømmelsesmetoder undersøges. Gennem teoretisk analyse og eksperimentel verifikation forbedres ikke kun pålideligheden af voltageoverførernes måleresultater, men der gives også en solid garanti for den stabile drift af kraftsystemet.