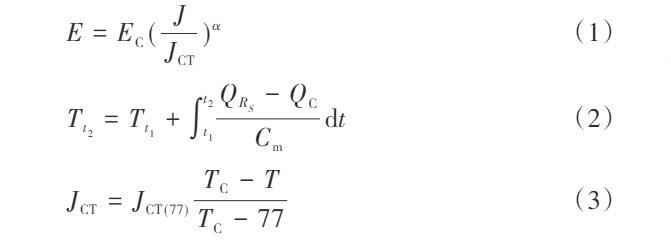Studia nad optymalnym doborem oporu rezystancyjnych nadprzewodzących ograniczników przepływu krótkiego dla elastycznych systemów przesyłowych prądu stałego

1 Odporny superprzewodnikowy ogranicznik prądu z przewrotki

1.1 Zasada działania

Wraz z rozszerzaniem się skali sieci energetycznych, zdolność do krótkiego zwarcia w krajowych systemach energetycznych szybko rośnie, co stwarza istotne wyzwania dla budowy i eksploatacji sieci. Aby rozwiązać problem zbyt dużych prądów zwarciowych, rosnąca uwaga skupia się na superprzewodnikowych ogranicznikach prądu zwarciowego (SFCL) opartych na zasadzie superprzewodnictwa. W zależności od ich charakterystyki tłumienia podczas przejścia do stanu o wysokim oporze, SFCL można podzielić na typy odpornościowe i indukcyjne.

Spośród nich, odporny superprzewodnikowy ogranicznik prądu zwarciowego cechuje się prostą konstrukcją, kompaktnymi rozmiarami i niewielką masą, z jasną zasadą działania. Po wejściu do stanu o wysokim oporze jego impedancja ograniczająca prąd gwałtownie wzrasta, zapewniając silną zdolność do tłumienia prądu zwarciowego. Ponadto, pojemność urządzenia może być elastycznie dostosowana poprzez szeregowe lub równoległe konfiguracje superprzewodników. W ostatnich latach osiągnięto przełom w materiałach superprzewodzących przy temperaturze pokojowej, co sprawia, że zarówno środowisko akademickie, jak i branża, szeroko uważa odporne SFCL za główny kierunek rozwoju w przyszłości.

Prąd krytyczny, pole magnetyczne krytyczne i temperatura krytyczna są kluczowymi parametrami fizycznymi określającymi, czy superprzewodnik znajduje się w stanie superprzewodzącym. Gdy którykolwiek z tych parametrów przekracza swoją wartość krytyczną, superprzewodnik przechodzi ze stanu superprzewodzącego do stanu zgaszonego. Proces zgaszenia składa się z dwóch etapów: najpierw stan przepływu strumienia magnetycznego, a następnie normalny stan oporny. Gdy gęstość prądu przez superprzewodnik przekracza jego gęstość prądu krytycznego, superprzewodnik wchodzi do stanu przepływu strumienia magnetycznego.

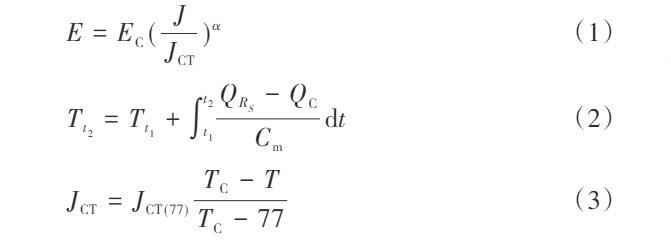
Gdzie: E to natężenie pola elektrycznego; EC to natężenie pola elektrycznego krytycznego; J to gęstość prądu; JCT to gęstość prądu krytycznego; α to stała; Tt1 i Tt2 to temperatury superprzewodnika w chwilach t1 i t2 odpowiednio; QRS to ciepło wygenerowane przez opór Rs od t1 do t2; QC to wymiana ciepła między superprzewodnikiem a jego otoczeniem w przedziale czasu t1–t2; Cm to ciepło właściwe superprzewodnika; JCT(77) to gęstość prądu krytycznego przy 77 K (77 K jest temperaturą środowiska azotu ciekłego); TC to temperatura krytyczna; T to temperatura superprzewodnika.

Zgodnie z równaniem (1), gdy gęstość prądu J wzrasta, natężenie pola elektrycznego E superprzewodnika rośnie szybko, prowadząc do wzrostu jego oporu. Zwiększenie oporu wzmacnia efekt termiczny, a zgodnie z równaniem (2), temperatura superprzewodnika również wzrasta.

Z równania (3) wynika, że wzrost temperatury zmniejsza gęstość prądu krytycznego, co dalszy wzrost natężenia pola elektrycznego E, powodując ciągły wzrost oporu superprzewodnika. Gdy opór rośnie, ciepło generowane przez superprzewodnik stopniowo wyrównuje się z ciepłem oddawanym do otoczenia, a temperatura stabilizuje się, kończąc w stanie stałego oporu normalnym.

1.2 Zastosowanie R-SFCL w elastycznych systemach DC

W elastycznych systemach transmisji DC, prąd DC nie ma naturalnych przecięć. Gdy wystąpi awaria zwarciowa, prąd zwarciowy rośnie szybko, stanowiąc poważne zagrożenie dla urządzeń elektrycznych w systemie. Aby zapewnić niezawodność systemu, przekaźniki muszą szybko izolować linie z uszkodzeniami. Obecnie, przekaźniki DC nie spełniają jeszcze pełni wymogów praktycznych zastosowań.

Gdy wystąpi awaria po stronie DC, zwykle przerywane są przekaźniki po stronie AC, ale to nieuchronnie prowadzi do zamknięcia stacji przekształtniczej, a urządzenia elektroniczne mogą ulec uszkodzeniu z powodu nadmiernego prądu w tym okresie. Ochrona DC musi zakończyć cały cykl ochrony w ciągu kilku milisekund, podczas gdy najkrótszy czas działania przekaźników AC wynosi zwykle 50 ms, co sprawia, że nie są one w stanie skutecznie chronić urządzeń elektronicznych w systemie.

Obecna technologia umożliwia R-SFCL osiągnięcie normalnego stanu opornego w ciągu około 3 ms. Odporny superprzewodnikowy ogranicznik prądu zwarciowego przełącza się do stanu ograniczającego prąd znacznie szybciej niż działa ochrona relacyjna, i osiąga stan wysokiego impedancji przed usunięciem uszkodzenia, co skutecznie redukuje prąd zwarciowy.

2 Charakterystyka uszkodzeń DC w elastycznych systemach DC

Lokalizacja punktu uszkodzenia wpływa tylko na impedancję systemu, a nie na ścieżkę prądu ani podstawowe cechy uszkodzenia zwarciowego. Ze względu na wygodę modelowania, uszkodzenie umieszczane jest w środku linii DC i zakłada się, że jest to zwarciowe metalowe. Budowany jest model symulacji dwubiegunowego elastycznego systemu DC oraz model R-SFCL za pomocą PSCAD/EMTDC, z nominalnym napięciem systemu ±110 kV i mocą nominalną 75 MW. Lokalizacja instalacji R-SFCL jest pokazana na rys. 1.

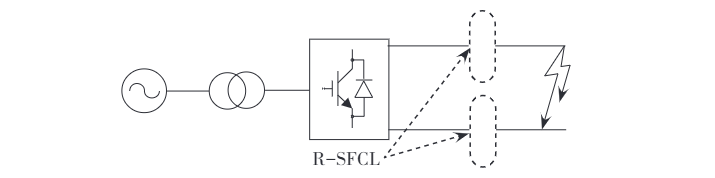
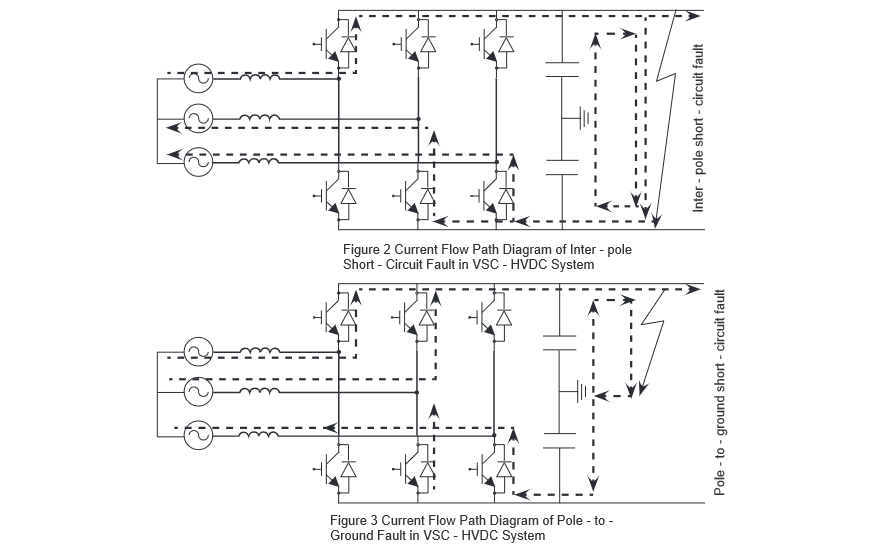
Gdy wystąpi uszkodzenie zwarciowe DC, IGBT jest wykrywany i natychmiast blokowany przez funkcję blokady po wykryciu prądu zwarciowego. Jednak diody połączone równolegle z IGBT i liniami transmisyjnymi tworzą niekontrolowany most prostowniczy, pozwalający na kontynuację komutacji nawet po zablokowaniu IGBT. Uszkodzenie zwarciowe biegun-biegun DC można podzielić głównie na trzy etapy: Pierwszy etap następuje bezpośrednio po uszkodzeniu, podczas którego kondensator po stronie DC szybko rozładowuje się, a prąd DC wzrasta do swojej wartości maksymalnej w ciągu kilku milisekund.

W drugim etapie, po spadku napięcia kondensatora do zera, prąd płynący przez diody może osiągnąć ponad dziesięciokrotność ich nominalnej wartości, co czyni urządzenia elektroniczne bardzo podatnymi na uszkodzenia. W trzecim etapie, gdy prąd zwarciowy DC spada poniżej prądu sieci AC, sieć AC zaczyna podawać prąd zwarciowy do punktu uszkodzenia DC. Uszkodzenie zwarciowe DC do ziemi nie ma drugiego etapu, w innych przypadkach jego cechy są podobne do uszkodzenia biegun-biegun.

Podczas podawania prądu AC, prąd przez diody jest około dziesięciokrotnością ich nominalnej wartości. Ścieżki prądu dla tych dwóch rodzajów uszkodzeń zwarciowych DC w elastycznym systemie DC są przedstawione na rys. 2 i rys. 3. Instalacja R-SFCL wzdłuż ścieżki prądu zwarciowego może szybko zwiększyć opór obwodu zwarciowego, zapewniając więcej czasu na usunięcie uszkodzenia i zmniejszając wymagania dotyczące naturalnego czasu otwarcia i zdolności przerywania przekaźników DC.

3 Analiza symulacyjna

Za pomocą programu symulacyjnego PSCAD/EMTDC, opracowany model R-SFCL jest zintegrowany z utworzonym modelem symulacji dwubiegunowego elastycznego systemu DC o mocy 75 MW w celu weryfikacji. Wydajność ograniczania prądu w przypadku uszkodzenia zwarciowego biegun-biegun DC jest przedstawiona na rys. 4, a w przypadku uszkodzenia zwarciowego linii DC do ziemi na rys. 5. Jak widać na rys. 4 i rys. 5, maksymalny prąd zwarciowy maleje wraz ze wzrostem oporu stanu normalnego. Jest oczywiste, że opór R-SFCL i maksymalny prąd zwarciowy po instalacji wykazują pewną funkcjonalną zależność degradacyjną.

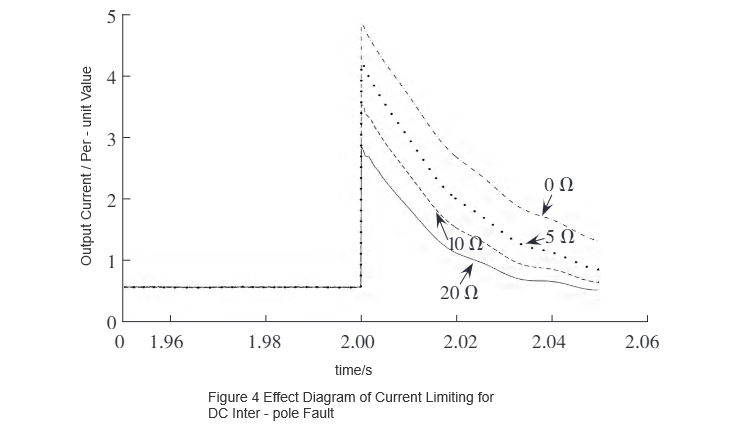
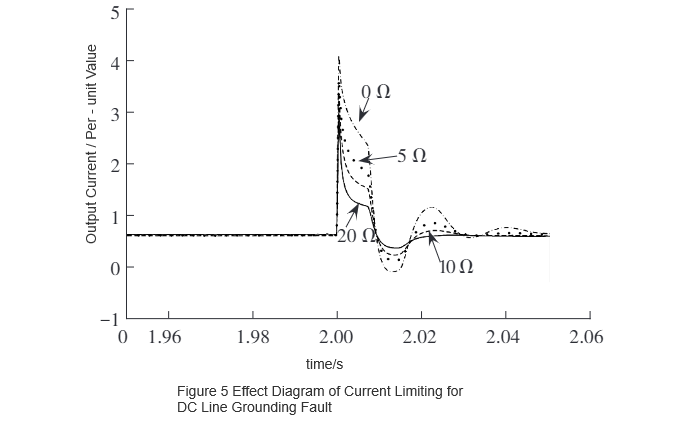
Aby rozszerzyć zakres zastosowań, oryginalny model był stopniowo skalowany na podstawie trzech pojemności systemowych: 75 MW, 150 MW i 300 MW. W warunkach zwarciowego uszkodzenia biegun-biegun DC i zwarciowego uszkodzenia linii DC do ziemi, badano zależność między wartością oporu stanu normalnego R-SFCL a maksymalnym prądem zwarciowym, uzyskując wartości maksymalne prądów zwarciowych. Wyniki są przedstawione na rys. 6 i rys. 7.

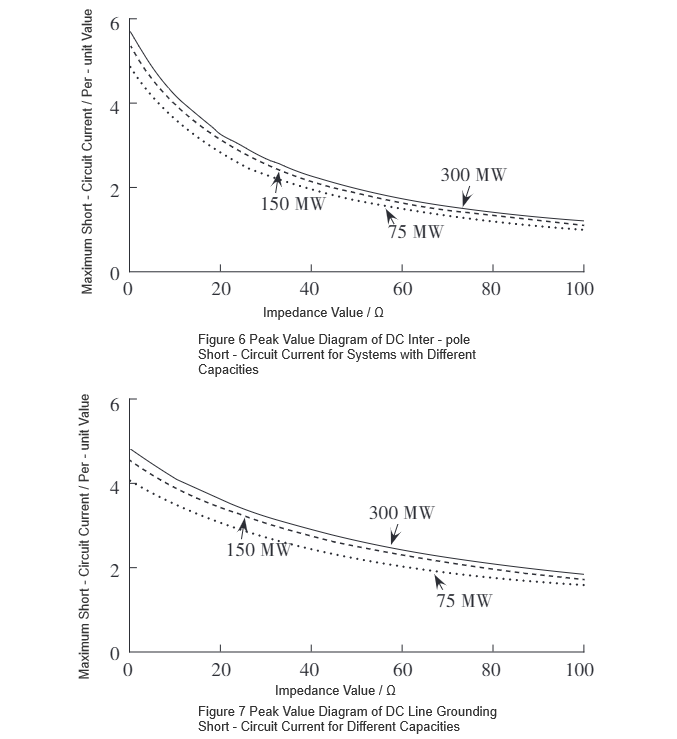
Korzystając z funkcji dopasowania krzywych w MATLAB, krzywe na rys. 6 i rys. 7 zostały dopasowane, otrzymując funkcjonalne wyrażenia postaci f(x) = ae⁻ᵇˣ + c, z konkretnymi parametrami wymienionymi w tabeli 1. Pochodna dopasowanej funkcji wynosi f'(x) = -abe⁻ᵇˣ. Z tabeli 1 można zauważyć, że dla tego samego typu uszkodzenia, parametr b pozostaje prawie stały, podczas gdy parametr a wzrasta wraz z pojemnością systemu. Ponieważ b jest stosunkowo małe, wyrażenia nachylenia krzywych dla tego samego typu uszkodzenia są prawie identyczne.Dlatego R-SFCL o tym samym oporze stanu normalnego mają tę samą szybkość zmiany maksymalnego prądu zwarciowego w różnych pojemnościach systemowych dla tego samego typu uszkodzenia, co wskazuje na spójną wydajność ograniczania prądu.

Ponadto, w miarę liniowego wzrostu oporu stanu normalnego R-SFCL, jego skuteczność ograniczania prądu stopniowo maleje. Na podstawie nachyleń krzywych na rys. 6 i rys. 7, optymalny zakres oporu stanu normalnego R-SFCL, aby maksymalizować szybkość redukcji maksymalnego prądu zwarciowego, wynosi 0–10 Ω.

4 Wnioski

Instalacja R-SFCL na stronie DC stacji przekształtniczej w elastycznym systemie transmisji DC może skutecznie zmniejszyć prądy zwarciowe DC. W miarę liniowego wzrostu wartości oporu R-SFCL, jego skuteczność ograniczania prądu stopniowo maleje. Biorąc pod uwagę obecny stan badań, koszty inżynieryjne i wymagania dotyczące powierzchni, zaleca się, aby optymalny zakres oporu stanu normalnego R-SFCL wynosił 0–10 Ω.