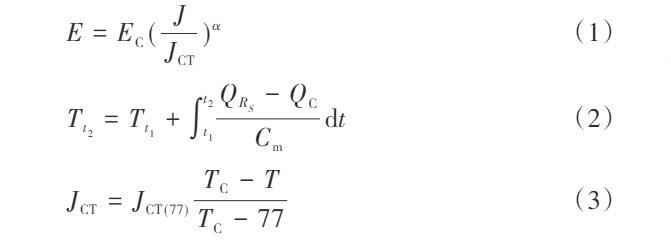Studie o optimálním výběru odporu pro odporové nadproudové omezovače s využitím supravodičů pro flexibilní systémy přenosu střídavého proudu

1 Odporový nadproudový omezovač proudů

1.1 Princip fungování

S rozšiřujícími se měřítky elektrických sítí se rychle zvyšuje krátkozaměrná kapacita domácích elektrických systémů, což představuje významné výzvy pro stavbu a provoz sítí. Pro řešení problému s příliš vysokými krátkozaměrnými proudy získávají stále více pozornosti nadproudové omezovače proudů (SFCLs) založené na principu nadproudovosti. Podle jejich tlumivých charakteristik při přechodu do vysoko-odporového stavu lze SFCLs rozdělit na odporové a indukční typy.

Mezi nimi má odporový nadproudový omezovač proudu jednoduchou konstrukci, kompaktní rozměry a malou hmotnost, s jasným principem fungování. Jakmile vstoupí do vysoko-odporového stavu, jeho omezovací impedance se prudce zvýší, poskytujíc tak silnou schopnost potlačovat chybové proudy. Kromě toho lze kapacitu zařízení flexibilně upravit sériovým nebo paralelním uspořádáním nadproudových materiálů. V posledních letech se objevily průlomové výsledky v oblasti nadproudových materiálů pracujících při pokojové teplotě, což vedlo jak akademické, tak průmyslové kruhy k tomu, že odporové SFCLs jsou považovány za hlavní směr budoucího vývoje.

Kritický proud, kritické magnetické pole a kritická teplota jsou klíčové fyzikální parametry pro určení, zda je nadproudový materiál v nadproudovém stavu. Pokud kterýkoliv z těchto parametrů překročí svou kritickou hodnotu, přechází nadproudový materiál ze stavu nadproudového do stavu uhašeného. Proces uhašení se skládá ze dvou fází: nejprve stav toku fluence, následovaný normálním odporovým stavem. Když hustota proudu procházejícího nadproudovým materiálem překročí jeho kritickou hustotu proudu, vstupuje nadproudový materiál do stavu toku fluence.

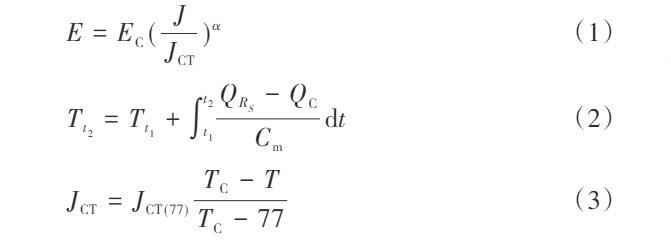
Kde: E je intenzita elektrického pole; EC je kritická intenzita elektrického pole; J je hustota proudu; JCT je kritická hustota proudu; α je konstanta; Tt1 a Tt2 jsou teploty nadproudového materiálu v časech t1 a t2; QRS je teplo vygenerované odporem Rs od t1 do t2; QC je teplo vyměňované mezi nadproudovým materiálem a jeho okolím během časového intervalu t1–t2; Cm je specifická tepelná kapacita nadproudového materiálu; JCT(77) je kritická hustota proudu při 77 K (77 K je teplota prostředí tekutého dusíku); TC je kritická teplota; T je teplota nadproudového materiálu.

Podle rovnice (1), když se zvýší hustota proudu J, intenzita elektrického pole E nadproudového materiálu rychle stoupá, což vede ke zvýšení jeho odporu. Zvýšený odpor zesiluje tepelný efekt, a jak ukazuje rovnice (2), teplota nadproudového materiálu se odpovídajícím způsobem zvyšuje.

Z rovnice (3) je známo, že zvýšení teploty snižuje kritickou hustotu proudu, což dále zvyšuje intenzitu elektrického pole E, což způsobuje, že odpor nadproudového materiálu neustále roste. S rostoucím odporem se teplo generované nadproudovým materiálem postupně vyrovná s teplem odvedeným do okolí, a teplota se stabilizuje, nakonec dosahujíc konstantního odporového normálního stavu.

1.2 Použití R-SFCL v flexibilních DC systémech

V flexibilních DC přenosových systémech chybí DC proudu přirozené nulové přechody. Jakmile dojde k krátkozaměrné chybě, chybový proud rychle stoupá, což představuje vážnou hrozbu pro elektrické zařízení v systému. Pro zajištění spolehlivosti systému musí obvodové přerušovače rychle izolovat vadnou linku. Současné DC obvodové přerušovače zatím plně nevyhovují praktickým požadavkům.

Při chybě na straně DC se obvykle vyhazují přerušovače na straně AC, ale to nevyhnutelně vede k vypnutí stanic převodníků, a během této doby mohou být poškozeny elektronické součástky nadměrným proudem. DC ochrana musí dokončit celou ochrannou sekvenci během několika milisekund, zatímco nejrychlejší čas reakce AC obvodových přerušovačů je obvykle 50 ms, což je nedostatečné pro efektivní ochranu elektronických součástek v systému.

Současná technologie umožňuje R-SFCL dosáhnout normálního odporového stavu během přibližně 3 ms. Odporový nadproudový omezovač proudu přechází do omezovacího stavu mnohem rychleji, než funguje relé ochrana, a dosahuje vysoko-odporového stavu před vyřízením chyby, což efektivně snižuje krátkozaměrný proud.

2 Charakteristika DC chyb v flexibilních DC systémech

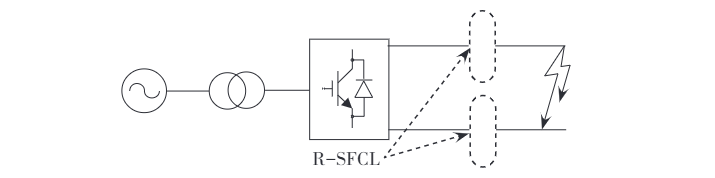
Umístění bodu chyby ovlivňuje pouze impedanci systému, nikoli cestu proudu nebo základní charakteristiky krátkozaměrné chyby. Pro snazší modelování je chyba umístěna uprostřed DC linky a předpokládá se, že jde o kovovou krátkozaměrnou spojnici. Pomocí PSCAD/EMTDC byl vytvořen simulovaný model dvojkoncevého flexibilního DC systému a model R-SFCL, s nominálním napětím systému ±110 kV a nominální výkon 75 MW. Umístění R-SFCL je zobrazeno na obrázku 1.

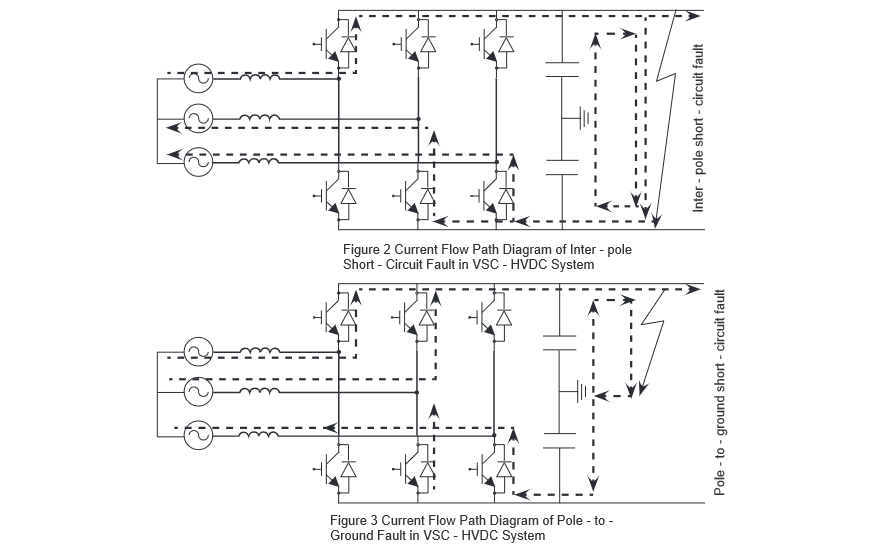
Při výskytu DC krátkozaměrné chyby je IGBT detekován a okamžitě blokován pomocí funkce blokování po detekci chybového proudu. Nicméně, diody zapojené paralelně s IGBT a přenosové linky tvoří nekontrolní mostový obvod, což umožňuje komutaci i po blokování IGBT. DC pol-pole krátkozaměrná chyba se dělí především na tři fáze: První fáze nastává okamžitě po vzniku chyby, kdy DC kondenzátor rychle vybíjí a DC proud stoupá do svého vrcholového hodnoty během několika milisekund.

Ve druhé fázi, po poklesu napětí kondenzátoru na nulu, může proud procházející diodami dosáhnout více než desetinásobku jejich nominálního proudu, což způsobuje, že elektronické součástky jsou velmi náchylné k poškození. V třetí fázi, když DC krátkozaměrný proud klesne pod proud AC sítě, začíná AC síť dodávat krátkozaměrný proud do místa DC chyby. DC zemní chyba nemá druhou fázi; jinak jsou její charakteristiky podobné jako u pol-pole chyby.

Během doplňování proudu z AC sítě je proud procházející diodami přibližně desetkrát větší než jejich nominální proud. Cesty proudu pro tyto dva typy DC krátkozaměrných chyb v flexibilním DC systému jsou znázorněny na obrázku 2 a 3. Instalace R-SFCL podél cesty chybového proudu může rychle zvýšit odpor krátkozaměrného obvodu, což poskytuje více času pro vyřízení chyby a snižuje požadavky na vlastní čas otevření a vypínací kapacitu DC obvodových přerušovačů.

3 Simulační analýza

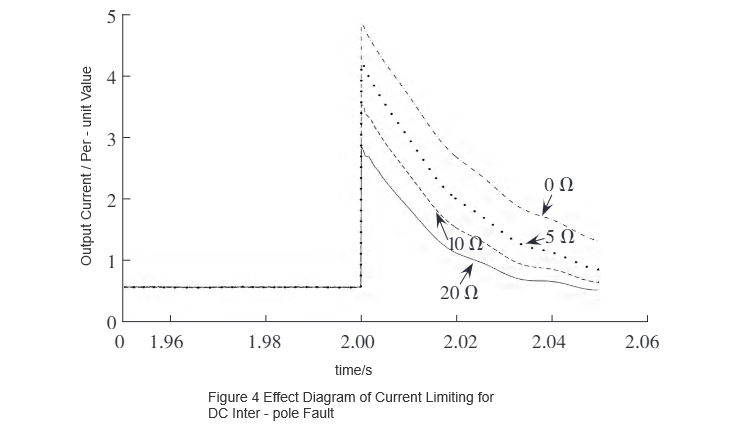
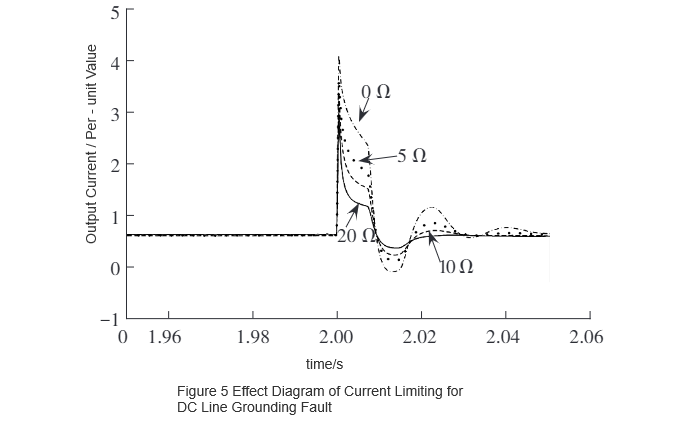
Pomocí simulačního softwaru PSCAD/EMTDC byl vyvinutý model R-SFCL integrován do již vytvořeného simulovaného modelu dvojkoncevého flexibilního DC systému s výkonem 75 MW pro ověření. Omezovací výkon při DC pol-pole chybě je znázorněn na obrázku 4, a při DC line-to-ground chybě na obrázku 5. Jak je vidět na obrázku 4 a 5, vrcholový chybový proud klesá s rostoucím odporem normálního stavu. Je zřejmé, že odpor R-SFCL a vrcholový chybový proud po instalaci mají určitou degradující funkční relaci.

Pro rozšíření oblasti použití byl původní model postupně škálován na základě tří systémových kapacit: 75 MW, 150 MW a 300 MW. Za podmínek DC pol-pole krátkozaměrné chyby a DC line-to-ground krátkozaměrné chyby byla studována vztah mezi hodnotou odporu normálního stavu R-SFCL a vrcholovým krátkozaměrným proudem získáním vrcholových hodnot krátkozaměrných proudů. Výsledky jsou znázorněny na obrázku 6 a 7.

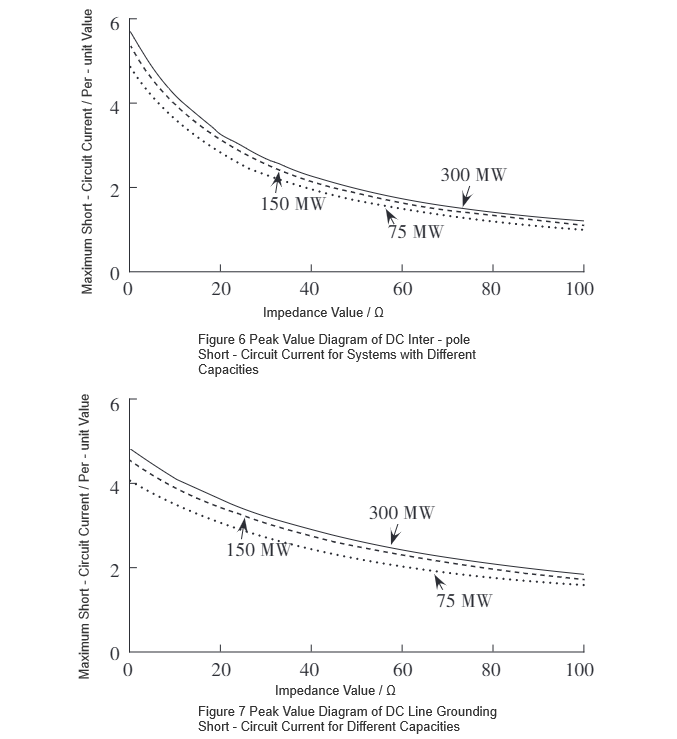
Pomocí funkce křivkového proložení v MATLABu byly křivky na obrázku 6 a 7 proloženy, což vedlo k funkčním výrazům ve tvaru f(x) = ae⁻ᵇˣ + c, s konkrétními parametry uvedenými v tabulce 1. Derivace proložené funkce dává f'(x) = -abe⁻ᵇˣ. Z tabulky 1 lze pozorovat, že pro stejný typ chyby zůstává parametr b téměř konstantní, zatímco parametr a roste s kapacitou systému. Protože b je relativně malé, jsou sklonové výrazy křivek pro stejný typ chyby téměř identické.Proto R-SFCL s tím samým odporem normálního stavu mají stejnou rychlost změny vrcholového chybového proudu v různých systémových kapacitách pro stejný typ chyby, což naznačuje konzistentní omezovací výkon.

Dále, s lineárním nárůstem odporu normálního stavu R-SFCL jeho omezovací účinnost postupně slábne. Na základě sklonů křivek na obrázku 6 a 7 je optimální rozsah odporu normálního stavu R-SFCL pro maximalizaci rychlosti snížení vrcholového chybového proudu 0–10 Ω.

4 Závěr

Instalace R-SFCL na straně DC výstupu stanice převodníku v flexibilním DC přenosovém systému může efektivně snížit DC krátkozaměrné chybové proudy. S lineárním nárůstem hodnoty odporu R-SFCL jeho omezovací účinek postupně slábne. Z hlediska aktuálního výzkumu, inženýrských nákladů a požadavků na plochu pozemku se doporučuje, aby optimální rozsah odporu normálního stavu R-SFCL byl 0–10 Ω.