Étude sur la sélection optimale de la résistance des limiteurs de courant de faute à supraconducteur résistif pour les systèmes de transmission continue flexible

1 Limiteur de courant de faute supraconducteur résistif

1.1 Principe de fonctionnement

Alors que l'échelle des réseaux électriques continue de s'élargir, la capacité de court-circuit des systèmes électriques nationaux augmente rapidement, posant des défis significatifs à la construction et à l'exploitation du réseau. Pour répondre au problème de courants de court-circuit excessifs, les limiteurs de courant de faute supraconducteurs (SFCL) basés sur les principes de supraconductivité reçoivent une attention croissante. En fonction de leurs caractéristiques d'amortissement lors de la transition vers l'état de haute résistance, les SFCL peuvent être classés en types résistifs et inductifs.

Parmi ceux-ci, le limiteur de courant de faute supraconducteur résistif se distingue par sa structure simple, sa compacité et son poids léger, avec un principe de fonctionnement clair. Une fois qu'il entre dans l'état de haute résistance, son impédance limitatrice de courant augmente fortement, offrant une capacité de suppression puissante des courants de faute. De plus, la capacité de l'appareil peut être ajustée de manière flexible par le biais de configurations en série ou en parallèle des supraconducteurs. Ces dernières années, des percées dans les matériaux supraconducteurs à température ambiante ont émergé, conduisant la communauté académique et industrielle à considérer largement les SFCL résistifs comme la principale direction pour le développement futur.

Le courant critique, le champ magnétique critique et la température critique sont des paramètres physiques clés pour déterminer si un supraconducteur est dans l'état supraconducteur. Lorsque l'un de ces paramètres dépasse sa valeur critique, le supraconducteur passe de l'état supraconducteur à l'état de quench. Le processus de quench se compose de deux étapes : d'abord, l'état de flux, suivi de l'état résistif normal. Lorsque la densité de courant à travers le supraconducteur dépasse sa densité de courant critique, le supraconducteur entre dans l'état de flux.

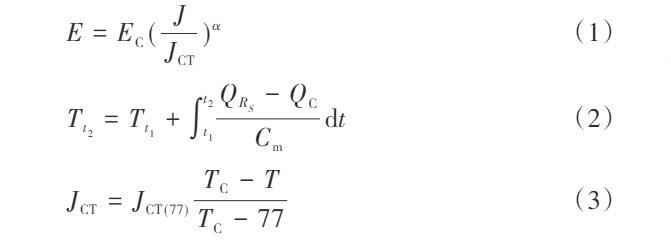
Où : E est l'intensité du champ électrique ; EC est l'intensité critique du champ électrique ; J est la densité de courant ; JCT est la densité de courant critique ; α est une constante ; Tt1 et Tt2 sont les températures du supraconducteur aux temps t1 et t2, respectivement ; QRS est la chaleur générée par la résistance Rs de t1 à t2 ; QC est la chaleur échangée entre le supraconducteur et son environnement pendant l'intervalle de temps t1–t2 ; Cm est la capacité thermique massique du supraconducteur ; JCT(77) est la densité de courant critique à 77 K (77 K étant la température d'un environnement de nitrogène liquide) ; TC est la température critique ; T est la température du supraconducteur.

Selon l'équation (1), lorsque la densité de courant J augmente, l'intensité du champ électrique E du supraconducteur augmente rapidement, entraînant une augmentation de sa résistance. L'augmentation de la résistance renforce l'effet thermique, et comme indiqué dans l'équation (2), la température du supraconducteur augmente en conséquence.

D'après l'équation (3), on sait que l'augmentation de la température réduit la densité de courant critique, augmentant encore l'intensité du champ électrique E, ce qui fait augmenter continuellement la résistance du supraconducteur. Alors que la résistance augmente, la chaleur générée par le supraconducteur se stabilise progressivement avec la chaleur dissipée vers l'environnement, et la température se stabilise, atteignant finalement un état normal de résistance constante.

1.2 Application du R-SFCL dans les systèmes DC flexibles

Dans les systèmes de transmission DC flexibles, le courant continu ne présente pas de passages naturels par zéro. Une fois qu'une faute de court-circuit se produit, le courant de faute augmente rapidement, posant une menace grave pour les équipements électriques du système. Pour assurer la fiabilité du système, les disjoncteurs doivent isoler rapidement la ligne défectueuse. Actuellement, les disjoncteurs DC n'ont pas encore pleinement satisfait aux exigences d'application pratique.

Lorsqu'une faute se produit du côté DC, les disjoncteurs du côté AC sont généralement déclenchés, mais cela entraîne inévitablement l'arrêt de la station de conversion, et les dispositifs électroniques de puissance peuvent être endommagés en raison d'un courant excessif pendant cette période. La protection DC doit compléter l'ensemble de la séquence de protection en quelques millisecondes, alors que le temps de fonctionnement le plus rapide des disjoncteurs AC est généralement de 50 ms, ce qui les rend incapables de protéger efficacement les dispositifs électroniques de puissance du système.

La technologie actuelle permet aux R-SFCL d'atteindre l'état résistif normal en environ 3 ms. Le limiteur de courant de faute supraconducteur résistif passe à l'état de limitation de courant beaucoup plus rapidement que la protection par relais, et atteint l'état de haute impédance avant l'élimination de la faute, réduisant ainsi efficacement le courant de court-circuit.

2 Caractéristiques des fautes DC dans les systèmes DC flexibles

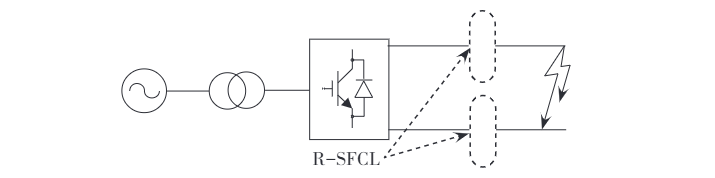
L'emplacement du point de faute affecte uniquement l'impédance du système, pas le chemin du courant ou les caractéristiques fondamentales de la faute de court-circuit. Pour des raisons de commodité de modélisation, la faute est placée au milieu de la ligne DC et supposée être un court-circuit métallique. Un modèle de simulation d'un système DC flexible à deux bornes et un modèle de R-SFCL sont construits à l'aide de PSCAD/EMTDC, avec une tension nominale du système de ±110 kV et une puissance nominale de 75 MW. L'emplacement d'installation du R-SFCL est montré dans la Fig. 1.

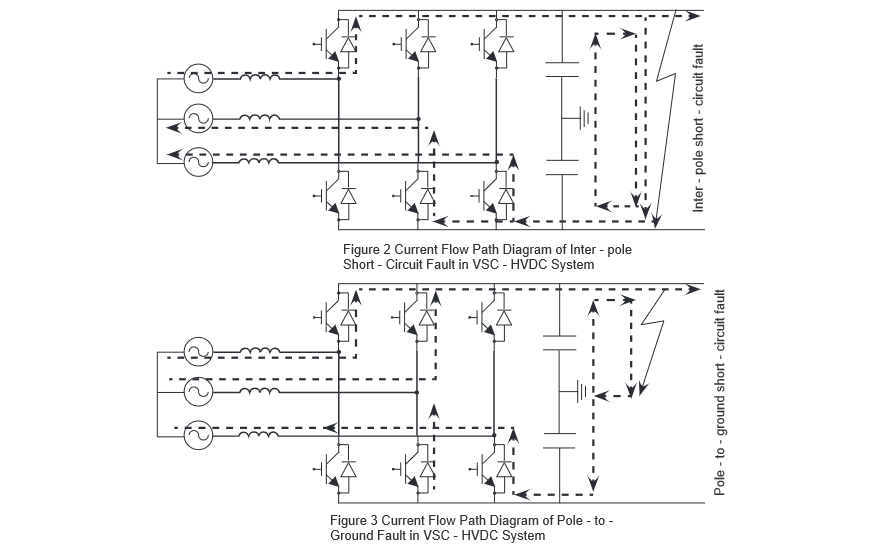
Lorsqu'une faute de court-circuit DC se produit, l'IGBT est détecté et immédiatement bloqué via sa fonction de blocage lors de la détection du courant de faute. Cependant, les diodes connectées en parallèle avec l'IGBT et les lignes de transmission forment un circuit redresseur non contrôlable, permettant la commutation de continuer même après le blocage de l'IGBT. Une faute de court-circuit entre pôles DC peut être principalement divisée en trois étapes : la première étape se produit immédiatement après la faute, pendant laquelle le condensateur du côté DC se décharge rapidement et le courant DC atteint sa valeur maximale en quelques millisecondes.

Dans la deuxième étape, après que la tension du condensateur diminue à zéro, le courant passant par les diodes peut atteindre plus de dix fois leur courant nominal, rendant les dispositifs électroniques de puissance très vulnérables à l'endommagement. Dans la troisième étape, lorsque le courant de court-circuit DC décroît en dessous du courant du réseau AC, le réseau AC commence à alimenter le courant de court-circuit vers le point de faute DC. Une faute de terre DC n'a pas de deuxième étape ; sinon, ses caractéristiques sont similaires à celles d'une faute entre pôles.

Lors de l'alimentation en courant AC, le courant de faute passant par les diodes est d'environ dix fois leur courant nominal. Les chemins de courant pour ces deux types de fautes de court-circuit DC dans le système DC flexible sont illustrés dans la Fig. 2 et la Fig. 3, respectivement. L'installation d'un R-SFCL le long du chemin de courant de faute peut augmenter rapidement la résistance de la boucle de court-circuit, fournissant plus de temps pour l'élimination de la faute et réduisant les exigences sur le temps d'ouverture intrinsèque et la capacité d'interruption des disjoncteurs DC.

3 Analyse de simulation

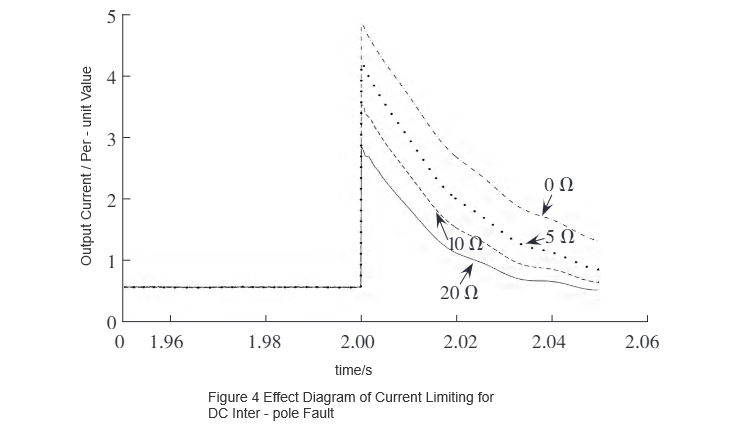
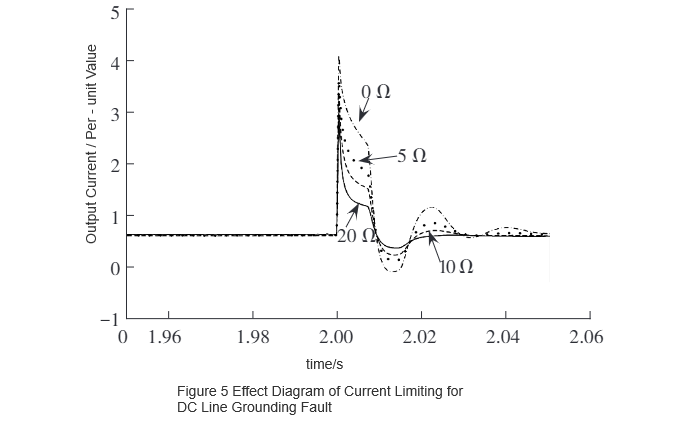
En utilisant le logiciel de simulation PSCAD/EMTDC, le modèle de R-SFCL développé est intégré dans le modèle de simulation d'un système DC flexible à deux bornes établi avec une capacité de 75 MW pour vérification. La performance de limitation de courant en cas de faute entre pôles DC est montrée dans la Fig. 4, et celle en cas de faute de ligne DC à la terre est montrée dans la Fig. 5. Comme on peut le voir dans la Fig. 4 et la Fig. 5, le courant de faute maximal diminue lorsque la résistance à l'état normal augmente. Il est évident que la résistance du R-SFCL et le courant de faute maximal après installation présentent une certaine relation fonctionnelle décroissante.

Pour élargir le champ d'application, le modèle original a été progressivement élargi sur la base de trois capacités de système : 75 MW, 150 MW et 300 MW. Dans les conditions de court-circuit entre pôles DC et de court-circuit de ligne DC à la terre, la relation entre la valeur de résistance à l'état normal du R-SFCL et le courant de court-circuit maximal a été étudiée en obtenant les valeurs maximales des courants de court-circuit. Les résultats sont montrés dans la Fig. 6 et la Fig. 7.

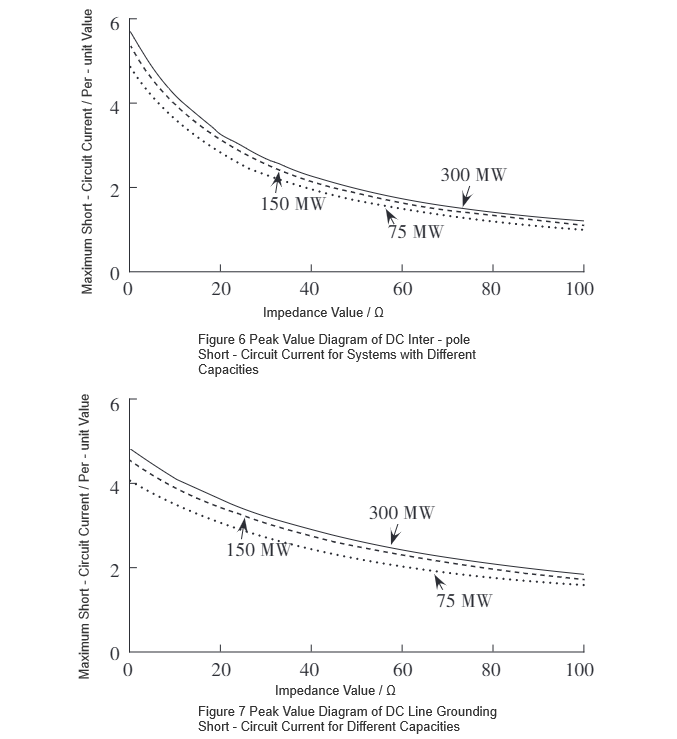
En utilisant la fonction d'ajustement de courbe dans MATLAB, les courbes de la Fig. 6 et de la Fig. 7 sont ajustées respectivement, aboutissant à des expressions fonctionnelles de la forme f(x) = ae⁻ᵇˣ + c, avec des paramètres spécifiques listés dans le Tableau 1. La dérivation de la fonction ajustée donne f'(x) = -abe⁻ᵇˣ. D'après le Tableau 1, on peut observer que pour le même type de faute, le paramètre b reste presque constant, tandis que le paramètre a augmente avec la capacité du système. Étant donné que b est relativement petit, les expressions de pente des courbes pour le même type de faute sont presque identiques.Ainsi, les R-SFCL avec la même résistance à l'état normal montrent le même taux de changement du courant de faute maximal pour différentes capacités de système pour le même type de faute, indiquant une performance de limitation de courant cohérente.

De plus, à mesure que la résistance à l'état normal du R-SFCL augmente linéairement, son efficacité de limitation de courant diminue progressivement. Sur la base des pentes des courbes de la Fig. 6 et de la Fig. 7, la plage optimale de résistance à l'état normal du R-SFCL pour maximiser le taux de réduction du courant de faute maximal est de 0–10 Ω.

4 Conclusion

L'installation d'un R-SFCL sur le côté sortie DC d'une station de conversion dans un système de transmission DC flexible peut réduire efficacement les courants de faute de court-circuit DC. À mesure que la valeur de résistance du R-SFCL augmente linéairement, son effet de limitation de courant diminue progressivement. En tenant compte de l'état actuel de la recherche, des coûts d'ingénierie et des exigences en termes de superficie, il est recommandé que la plage optimale de résistance à l'état normal pour le R-SFCL soit de 0–10 Ω.