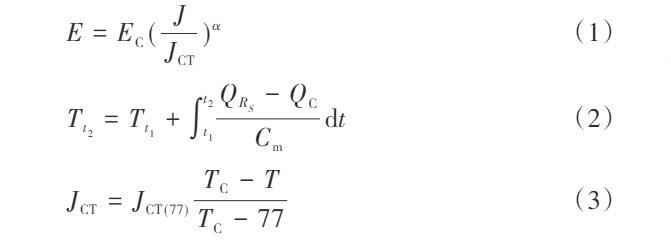Istraživanje optimalne selekcije otpora rezistivnih superprovodnih ograničivača struja za fleksibilne sisteme prenosa naponostaloga toka

1 Otpornički superprovodni ograničivač strujnog prekida

1.1 Način rada

Dok se mreže električne energije nastavljaju širiti, kapacitet kraćeg spoja u domaćim sistemima brzo raste, stvarajući značajne izazove za izgradnju i operativnost mreže. Da bi se rešila problema prekomjernih struja kraćeg spoja, superprovodni ograničivači strujnog prekida (SFCL) bazirani na principima superprovodnosti privlače sve veću pažnju. SFCL-ovi se mogu klasifikovati na otporničke i induktivne tipove, u zavisnosti od svojstava prigušenja pri prelazu u stanje visokog otpora.

Među njima, otpornički superprovodni ograničivač strujnog prekida ima jednostavnu strukturu, kompaktnu veličinu i sitnu težinu, sa jasnim načinom rada. Kada ulazi u stanje visokog otpora, njegov ograničujući impedans se oštro povećava, obezbeđujući snažnu sposobnost suzbijanja struje prekida. Takođe, kapacitet uređaja može biti fleksibilno podešen putem serijalnih ili paralelnih konfiguracija superprovodnika. U poslednjih godina, napredak u materijalima za superprovodnost pri sobnoj temperaturi doveo je do toga da akademski i industrijski krugovi široko smatraju otporničke SFCL-ove primarnim pravcem razvoja u budućnosti.

Kritična struja, kritično magnetno polje i kritična temperatura su ključni fizički parametri za određivanje da li je superprovodnik u superprovodnom stanju. Kada bilo koji od ovih parametara premaši svoju kritičnu vrednost, superprovodnik prelazi iz superprovodnog stanja u stanje zakvačenja. Proces zakvačenja se sastoji od dve faze: prvo, stanje toka fluksa, zatim normalno otporničko stanje. Kada gustoća struje koja prođe kroz superprovodnik premaši njegovu kritičnu gustoću struje, superprovodnik ulazi u stanje toka fluksa.

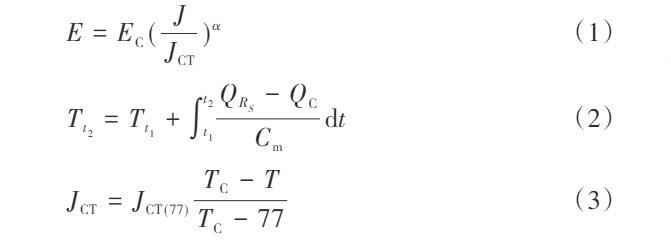
Gde: E predstavlja jačinu električnog polja; EC je kritična jačina električnog polja; J je gustoća struje; JCT je kritična gustoća struje; α je konstanta; Tt1 i Tt2 su temperature superprovodnika u trenucima t1 i t2, redom; QRS je toplota generisana otpornikom Rs od t1 do t2; QC je toplota menjana između superprovodnika i njegovog okruženja tokom vremenskog intervala t1–t2; Cm je specifična toplotna kapacitivnost superprovodnika; JCT(77) je kritična gustoća struje na 77 K (77 K je temperatura u okruženju tečnog azota); TC je kritična temperatura; T je temperatura superprovodnika.

Prema jednačini (1), kada se gustoća struje J poveća, jačina električnog polja E superprovodnika brzo raste, što dovodi do povećanja njegovog otpora. Povećan otpor pojačava toplinsku efektivnost, i kako pokazuje jednačina (2), temperatura superprovodnika se povećava.

Iz jednačine (3) se zna da se povećanje temperature smanjuje kritičnu gustoću struje, što dodatno povećava jačinu električnog polja E, uzrokujući da se otpor superprovodnika kontinualno povećava. Dok se otpor povećava, toplota generisana superprovodnikom postepeno dostiže ravnotežu sa toplotom disipiranom u okruženje, a temperatura se stabilizuje, eventualno dosežući konstantno-otporničko normalno stanje.

1.2 Primena R-SFCL-a u fleksibilnim DC sistemima

U fleksibilnim DC sistemima prijenosa, DC struja nema prirodne nule. Kada dođe do prekidne greške, struja prekida brzo raste, predstavljajući ozbiljan opasnost za električnu opremu u sistemu. Da bi se osigurala pouzdanost sistema, prekidnici moraju brzo izolovati prekidanu liniju. Trenutno, DC prekidnici još uvek nisu u potpunosti ispunili praktične zahteve.

Kada dođe do prekidne greške na DC strani, obično se aktiviraju prekidnici na AC strani, ali to neizbežno dovodi do gašenja pretvaračke stanice, a elektronička uređaja mogu biti oštećena zbog prekomjerne struje tokom ovog perioda. DC zaštita mora završiti celokupan zaštitni proces unutar nekoliko milisekundi, dok je najbrži vreme reagovanja AC prekidnika obično 50 ms, što ih čini neefikasnim za zaštitu elektroničke opreme u sistemu.

Trenutna tehnologija omogućava R-SFCL-ovima da dostignu normalno otporničko stanje unutar otprilike 3 ms. Otpornički superprovodni ograničivač strujnog prekida prelazi u stanje ograničenja struje mnogo brže nego reljayska zaštita, dostižući visoko-impedansno stanje pre ostvarenja prekida, time efikasno smanjujući struju prekida.

2 Karakteristike DC prekidne greške u fleksibilnim DC sistemima

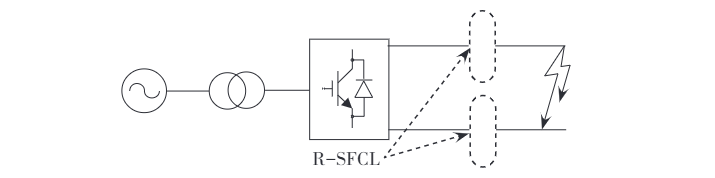
Lokacija tačke prekida utiče samo na impedans sistema, a ne na putanju struje ili fundamentalne karakteristike prekidne greške. Radi olakšavanja modeliranja, prekid se smesta na sredini DC linije i pretpostavlja se kao metalički prekid. Dvosmerni simulacioni model fleksibilnog DC sistema i model R-SFCL-a su izgrađeni koristeći PSCAD/EMTDC, sa sistemskim nominalnim naponom od ±110 kV i nominalnom snalom od 75 MW. Lokacija instalacije R-SFCL-a prikazana je na Slici 1.

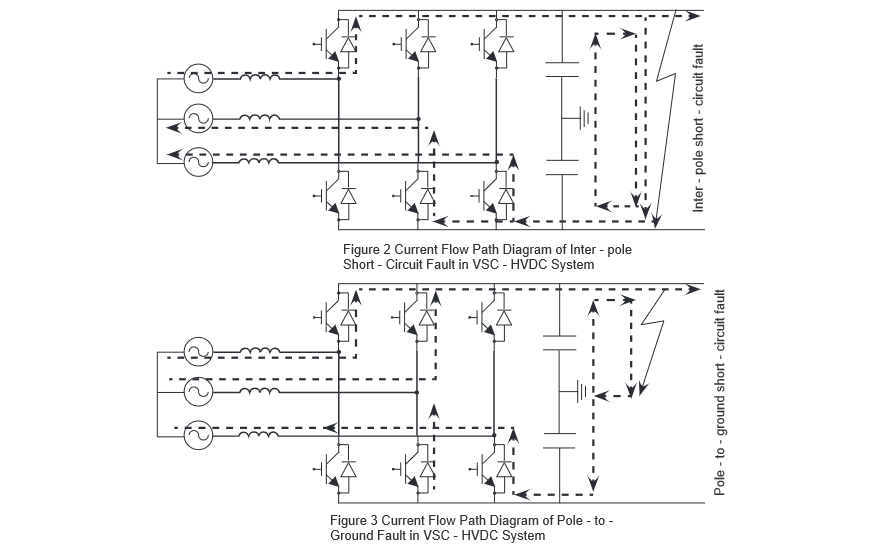
Kada dođe do DC prekidne greške, IGBT se detektuje i odmah blokira putem funkcije blokiranja nakon osetljivosti na struju prekida. Međutim, diode paralelne sa IGBT-om i prenosne linije formiraju nekontrolisanu mostovu pravougaonu šemu, omogućavajući nastavak komutacije čak i posle blokiranja IGBT-a. DC prekid između polova može se glavno podijeliti na tri faze: Prva faza se dešava odmah posle prekida, tokom koje DC kondenzator brzo ispražnjava, a DC struja raste do maksimalne vrednosti unutar nekoliko milisekundi.

U drugoj fazi, nakon što pada napon kondenzatora na nulu, struja koja prođe kroz diode može doseći više od deset puta njihovu nominalnu struju, čime elektronička uređaja postaju vrlo osetljiva na oštećenje. U trećoj fazi, kada DC prekidna struja opada ispod struje AC mreže, AC mreža počinje da unosi prekidnu struju u tačku DC prekida. DC prekid na zemlju ne ima drugu fazu; inače, njegove karakteristike su slične prekidu između polova.

Tokom unosa AC struje, struja koja prođe kroz diode iznosi približno deset puta njihovu nominalnu struju. Putanje struje za ova dva tipa DC prekidne greške u fleksibilnom DC sistemu su prikazane na Slici 2 i Slici 3, redom. Instalacija R-SFCL-a duž putanje struje prekida može brzo povećati otpor petlje prekida, pružajući više vremena za izvršenje prekida i smanjujući zahteve na intrinzično vreme otvaranja i prekidnu kapacitet DC prekidnika.

3 Simulacijska analiza

Korišćenjem simulacionog softvera PSCAD/EMTDC, razvijeni model R-SFCL-a je integrisan u postojeći simulacioni model dvosmernog fleksibilnog DC sistema sa kapacitetom od 75 MW za verifikaciju. Ograničujuće performanse pod DC prekidom između polova prikazane su na Slici 4, a one pod DC prekidom na zemlju na Slici 5. Kao što se može videti na Slici 4 i Slici 5, maksimalna struja prekida opada kako se normalni otpor povećava. Jasno je da otpor R-SFCL-a i maksimalna struja prekida nakon instalacije pokazuju određenu funkcionalnu vezu opadanja.

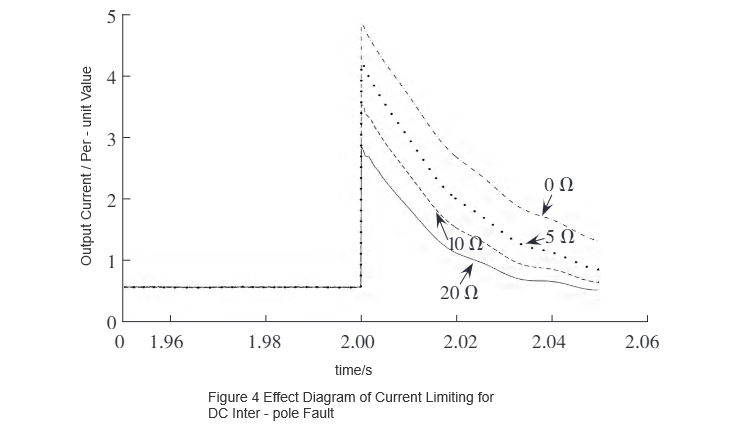
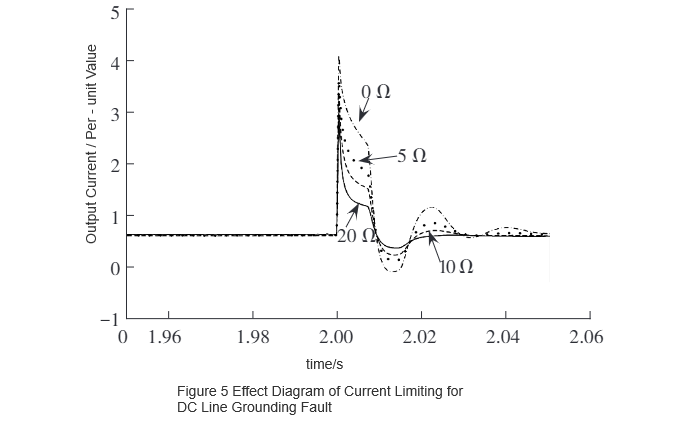
Da bi se proširio opseg primene, originalni model je postepeno skaliran na osnovu tri sistema kapaciteta: 75 MW, 150 MW i 300 MW. Pod uslovima DC prekida između polova i DC prekida na zemlju, proučavana je veza između normalne vrednosti otpora R-SFCL-a i maksimalne struje prekida, dobijanjem maksimalnih vrednosti struja prekida. Rezultati su prikazani na Slici 6 i Slici 7.

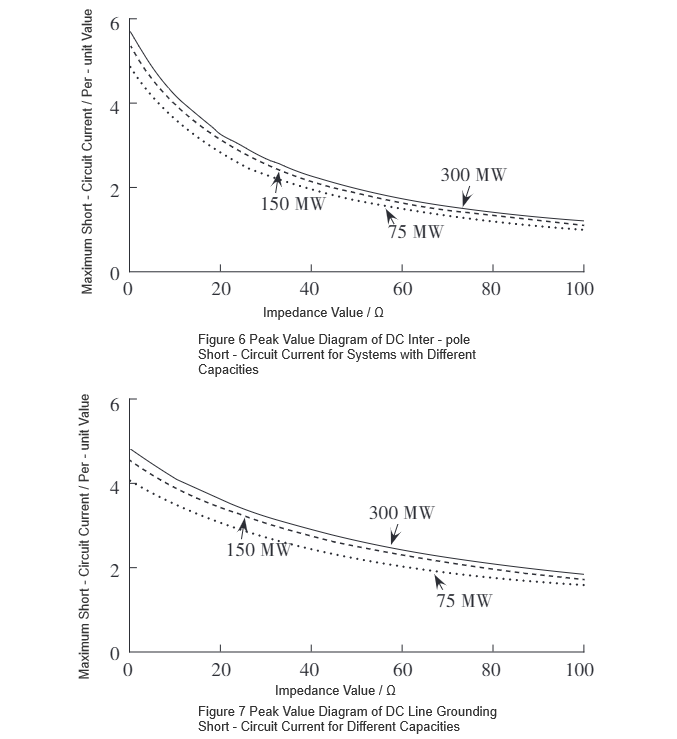
Korišćenjem funkcije aproksimacije krive u MATLAB-u, krive na Slici 6 i Slici 7 su aproksimirane, rezultirajući funkcionalnim izrazima oblika f(x) = ae⁻ᵇˣ + c, sa specifičnim parametrima navedenim u Tabeli 1. Diferenciranjem aproksimirane funkcije dobija se f'(x) = -abe⁻ᵇˣ. Iz Tabele 1 se može videti da za isti tip prekida, parametar b ostaje gotovo konstantan, dok parametar a raste sa kapacitetom sistema. Budući da je b relativno mali, izrazi nagiba krivih za isti tip prekida su skoro identični.Stoga, R-SFCL-ovi sa istim normalnim otporom pokazuju istu stopu promene maksimalne struje prekida na različitim sistemskim kapacitetima za isti tip prekida, ukazivajući na konzistentnu ograničujuću performansu.

Dodatno, kako se normalni otpor R-SFCL-a linearno povećava, njegova efikasnost ograničenja struje postepeno opada. Na osnovu nagiba krivih na Slici 6 i Slici 7, optimalni opseg normalnog otpora R-SFCL-a za maksimalnu stopu smanjenja maksimalne struje prekida je 0–10 Ω.

4 Zaključak

Instalacija R-SFCL-a na DC izlazu pretvaračke stanice u fleksibilnom DC sistemu prijenosa može efikasno smanjiti DC struje prekida. Kako se vrednost otpora R-SFCL-a linearno povećava, njegova efikasnost ograničenja struje postepeno opada. Uzimajući u obzir trenutni status istraživanja, inženjerske troškove i zahteve za površinom, preporučuje se da optimalni opseg normalnog otpora R-SFCL-a bude 0–10 Ω.