ग्रिड-से-पृथ्वी अनुकूलन परामानों मापनको लागि आवृत्ति विभाजन विधि

आवृत्ति विभाजन विधि द्वारा पोटेन्सियल ट्रान्सफोर्मर (PT) के ओपन डेल्टा भाग में अलग आवृत्ति के विद्युत धारा सिग्नल इंजेक्ट करके ग्रिड-से-माटी पैरामीटर्स को मापना संभव होता है।

यह विधि अनग्राउंड सिस्टमों के लिए लागू होती है; हालाँकि, जब एक अणुशोषण कुंडली द्वारा ग्राउंड किया गया न्यूट्रल बिंदु का ग्रिड-से-माटी पैरामीटर्स मापा जाता है, तो पहले से अणुशोषण कुंडली को संचालन से अलग कर देना चाहिए। इसका मापन सिद्धांत चित्र १ में दिखाया गया है।

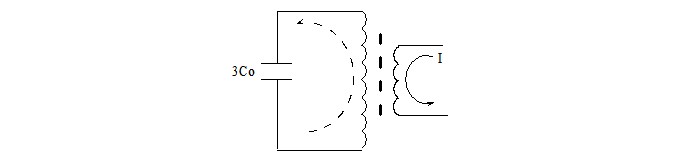
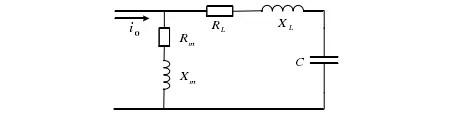
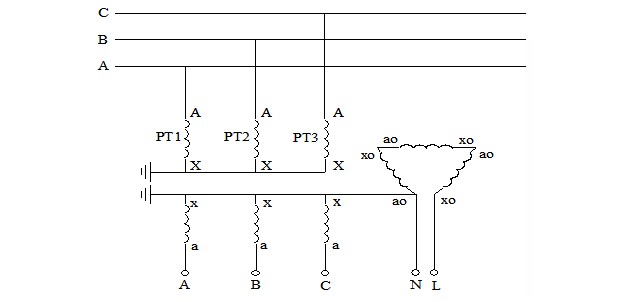चित्र १ में दिखाया गया है, जब PT के ओपन डेल्टा भाग से अलग आवृत्ति की धारा इंजेक्ट की जाती है, तो PT के उच्च वोल्टेज भाग पर शून्य-अनुक्रम धारा उत्पन्न होती है। चूँकि यह शून्य-अनुक्रम धारा तीन फेजों में समान परिमाण और दिशा की होती है, इसलिए यह विद्युत आपूर्ति भाग या लोड भाग से नहीं गुजर सकती और केवल PT और माटी की धारिता के माध्यम से लूप बना सकती है। इसलिए, चित्र १ का स्केमेटिक चित्र चित्र २ में दिखाए गए भौतिक मॉडल में आगे सरलीकृत किया जा सकता है।

PT के ओपन डेल्टा भाग से इंजेक्ट की गई अलग आवृत्ति की धारा एक ज्ञात राशि है, और इस भाग पर वोल्टेज सिग्नल को सीधे मापा जा सकता है।

चित्र २ के आधार पर चित्र ३ में दिखाए गए गणितीय मॉडल को स्थापित करने के बाद, मध्य वोल्टेज वितरण नेटवर्क की समतुल्य फेज-से-माटी धारिता की गणना PT के ट्रान्सफोर्मेशन अनुपात, दो अलग आवृत्तियों पर इंजेक्ट की गई धारा एम्प्लिट्यूड और वापसी वोल्टेज एम्प्लिट्यूड, तथा इन दो आवृत्तियों पर वापसी वोल्टेज सिग्नल और इंजेक्ट की गई धारा सिग्नल के बीच के फेज कोण अंतरों को संयोजित करके की जा सकती है।

मान लीजिए θₘ वोल्टेज सिग्नल और इंजेक्ट की गई धारा सिग्नल के बीच का फेज कोण अंतर, R वितरण नेटवर्क सिस्टम का फेज प्रतिरोध, और Zₘ वितरण नेटवर्क सिस्टम का फेज प्रतिबाधा है। तब:

इस प्रकार सरलीकृत किया जाता है:

वितरण नेटवर्क सिस्टम की फेज-से-माटी धारिता।

चित्र ३ में दिखाए गए भौतिक मॉडल के आधार पर, एक संगत गणितीय मॉडल स्थापित किया जा सकता है। सिग्नलों का निरीक्षण और मापन करके, तीन-फेज-से-माटी धारिता मान (3C) की माप की जा सकती है। हालाँकि, यह विधि मूल रूप से निश्चित त्रुटियों के साथ होती है।