Frekuentzia-banaketaren metodoak sakonpuntura-lerroetatik lurreko parametroen neurketa ahalbidetzen du potentzia-transformator (PT)ren delta irekian frekuentzia desberdina duen korronte bat inprimatzea bidez.
Metodo hau erabil daiteke zati-sakontasunezko sistemetan; baina, sistema baten sakonpuntura-lerroetatik lurreko parametroak neurtzerakoan, non neurri-puntu neutroa arkuen supresio koil batez sakontasunez konektatuta dago, arkuen supresio koila lehendik kendu behar da. Neurrirako oinarrizko printzipioa Irudi 1ean erakusten da.
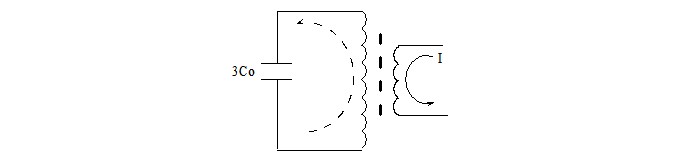
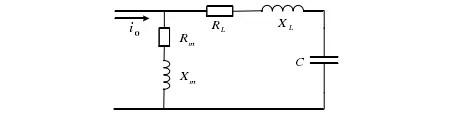
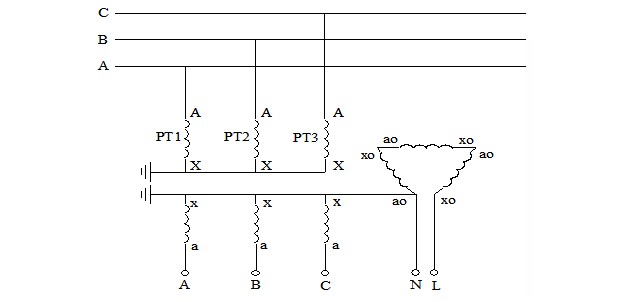Irudi 1ean ikus daitekeenez, PTren delta irekian frekuentzia desberdina duen korrontea inprimatzean, PTren sakonpuntura-lerroetan zero-sekuentziako korrontea sortzen da. Hainbat fasetan dituzten zero-sekuentziako korronte hori neurri-puntu eta karga-puntuetan ezin da igotzeko, PT eta lurreko kapazitatearekin bakarrik osa dezake itxura. Beraz, Irudi 1eko eskemak Irudi 2ko modelu fisikora sinplifikatu daitezke.
PTren delta irekian inprimatutako heterofrekuentziako korrontea ezaguna da, eta alde horretako tensio segnala direktxe neurtu daiteke.
Irudi 2tik Irudi 3ko matematika-modelua sortu ondoren, PTren aldaketa-erlazioa, bi frekuentzioko inprimatutako korronteen amplitudak eta itzulitako tensioen amplitudak, berota bi frekuentzietan itzulitako tensio segnalen eta inprimatutako korronte segnalen arteko angelu-desbiderak kontuan hartuta, banaketa-tarte sakonpuntura-lerroetako ekintza-berdina izango den kapazitatea kalkula daiteke.
Izan bitez θₘ tensio segnalaren eta inprimatutako korronte segnalaren arteko angelu-desbidera, R banaketa-tarte sisteman faseko erritantzia, eta Zₘ banaketa-tarte sisteman faseko impedimentua. Orduan:
Simplifikatu honela:
Banaketa-tarte sisteman faseko lurreko kapazitatea.
Irudi 3ko fisika-modeluari oinarrituz, matematika-modelu egokia sortu daiteke. Segnaleak detektatzean eta neurtzean, hiru fasetatik lurreko kapazitate-balioa (3C) neurtu daiteke. Baina metodo honek osozko errore batzuk ditu printzipiotik.
